已知二次函数 \(f(x)=ax^2+bx+c\) 满足 \(|f(0)|,|f(-1)|,|f(1)|\) 均不大于 \(1\),则当 \(x\in [-1,1]\) 时,\(|f(x)|\) 的最大值 \(M(a,b,c)\) 的最大值是________.

正确答案是\(\dfrac 54\).
分析与解 由于\[\begin{split}f(-1)&=a-b+c,\\f(0)&=c,\\f(1)&=a+b+c,\end{split}\]可得\[\begin{split}a&=\dfrac 12f(1)+\dfrac 12f(-1)-f(0),\\b&=\dfrac 12f(1)-\dfrac 12f(-1),\\c&=f(0),\end{split}\]因此\[\begin{split}|f(x)|&=\left|\left[\dfrac 12f(1)+\dfrac 12f(-1)-f(0)\right]\cdot x^2+\left[\dfrac 12f(1)-\dfrac 12f(-1)\right]\cdot x+f(0)\right|\\
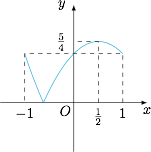
&=\left|f(1)\cdot \left(\dfrac 12x^2+\dfrac 12x\right)+f(-1)\cdot \left(\dfrac 12x^2-\dfrac 12x\right)+f(0)\cdot \left(1-x^2\right)\right|,\end{split}\]考虑到对称性,不妨设 \(x\in [0,1]\),于是\[\begin{split}|f(x)|&\leqslant |f(1)|\cdot \left(\dfrac 12x^2+\dfrac 12x\right)+|f(-1)|\cdot \left(\dfrac 12x-\dfrac 12x^2\right)+|f(0)|\cdot \left(1-x^2\right)\\&\leqslant \left(\dfrac 12x^2+\dfrac 12x\right)+\left(\dfrac 12x-\dfrac 12x^2\right)+\left(1-x^2\right)\\&=-x^2+x+1\\&\leqslant \dfrac 54.\end{split}\]事实上,当 \((a,b,c)=\left(1,-1,-1\right)\) 时,有 \(M(a,b,c)=\dfrac 54\),因此所求的最大值为 \(\dfrac 54\),如图.