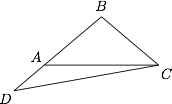
如图，$\triangle ABC$中，$BA=BC$，延长$BA$至点$D$使$BD=AC$，若$\angle BCD=50^\circ$，求证：$\angle B=100^\circ$．
分析与证明 设$BD=AC=2$，$\angle BDC=\theta$，则$$\angle DCA=25^\circ -\dfrac 12\theta,\angle BCA=25^\circ+\dfrac12\theta.$$在$\angle ADC$中应用正弦定理，可得\[\dfrac{AC}{\sin\angle BDC}=\dfrac{AD}{\sin\angle ACD}=\dfrac{AC-AB}{\sin\angle ACD},\]于是\[\dfrac{2}{\sin\theta}=\dfrac{2-\dfrac{1}{\cos\left(25^\circ+\dfrac 12\theta\right)}}{\sin\left(25^\circ-\dfrac 12\theta\right)},\]即\[2\sin\left(25^\circ-\dfrac 12\theta\right)\cdot \cos\left(25^\circ+\dfrac 12\theta\right)=2\cos\left(25^\circ+\dfrac 12\theta\right)\cdot \sin\theta-\sin\theta,\]积化和差，得\[2\sin\theta\cos\left(25^\circ+\dfrac 12\theta\right)=\sin 50^\circ.\]设等式左边函数为$f(\theta)$，则其导函数\[f'(\theta)=\cos \theta\cdot\cos \left(\dfrac 12\theta+25^\circ\right)\cdot \left[2-\tan \theta\cdot\tan \left(\dfrac 12\theta+25^\circ\right)\right],\]于是当$\theta$在不超过$50^\circ$时，$f(\theta)$单调递增，结合$f(30^\circ)=\sin 50^\circ$，可得$\theta=30^\circ$，因此$\angle B=100^\circ$．
注 本题来自尬题17，其中单调性的判断用到了$\tan 50^\circ<\sqrt 2$的结论，下面给出这个结论的两种证明．
方法一 考虑到$50^\circ$的三倍$150^\circ$是个特殊角，考虑三倍角公式解决问题．
要证明$\tan 50^\circ<\sqrt 2$即证明$\cos 50^\circ>\dfrac 1{\sqrt 3}$，考虑到$$\cos 3x=4\cos^3 x-3\cos x,$$知$\cos 50^\circ$是三次方程$$4x^3-3x+\dfrac {\sqrt 3}{2}=0$$的根，当$x=\dfrac 1{\sqrt 3}$时，方程左边小于零，所以$\cos 50^\circ>\dfrac 1{\sqrt 3}$．
方法二 利用正切函数图象的性质，因为$\tan 45^\circ=1,\tan 60^\circ=\sqrt 3$，所以$$\tan 50^\circ<\dfrac 13\tan 60^\circ+\dfrac 23\tan 45^\circ=\dfrac {2+\sqrt 3}{3}<\sqrt 2.$$