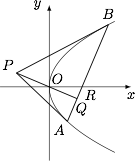
平面直角坐标系中$xOy$中,$P$是不在$x$轴上的一个动点,过$P$作抛物线$y^2=4x$的两条切线,切点设为$A,B$,且直线$PO\perp AB$于$Q$,$R$为直线$AB$与$x$轴的交点.
 (1) 求证:$R$是定点;
(1) 求证:$R$是定点;
(2) 求$\dfrac{PQ}{QR}$的最小值.
分析与解 (1) 设$P(m,n)$,则$AB:ny=2(x+m)$,根据题意,直线$PO$与直线$AB$垂直,于是\[\dfrac nm\cdot \dfrac 2n=-1,\]因此$m=-2$.进而$R(2,0)$为定点.
(2) 设直线$AB$的倾斜角为$\theta$,根据对称性,不妨设$\theta$为锐角.
法一 过$P$作$x$轴的垂线,设垂足为$H$,则$\triangle OPH$与$\triangle ORQ$相似,于是\[\begin{split} \dfrac{PQ}{QR}=&\dfrac{PO+OQ}{QR}\\=&\dfrac{\dfrac{2}{\sin\theta}+2\sin\theta}{2\cos\theta}\\=&\dfrac{3-\cos2\theta}{\sin2\theta},\end{split}\]令右侧代数式为$t$,则\[t\sin2\theta+\cos2\theta=3,\]于是\[\sqrt{1+t^2}\geqslant 3,\]解得$t\geqslant 2\sqrt 2$,等号当$\theta=\dfrac 12\arctan 2\sqrt 2$时取得.因此所求的最小值为$2\sqrt 2$.
法二 此时有直线$AB$的斜率\[\tan\theta=\dfrac 2n.\]而$PQ$为点$P$到直线$AB$的距离\[PQ=\dfrac{n^2+8}{\sqrt{4+n^2}},\]因此\[\begin{split} \dfrac{PQ}{QR}=&\dfrac{PQ}{OR}\cdot \dfrac{1}{\cos\theta}\\=&\dfrac{n^2+8}{2\sqrt{4+n^2}}\cdot \sqrt{\dfrac 4{n^2}+1}\\=&\dfrac n2+\dfrac 4n\geqslant 2\sqrt 2,\end{split} \]等号当$n=2\sqrt 2$时取得.因此所求的最小值为$2\sqrt 2$.
法三 因为 $m=-2$,所以直线 $PO$ 的斜率 $k_{1}=-\dfrac n2$,直线 $PR$ 的斜率 $k_{2}=-\dfrac n4$.
设 $\angle OPR=\alpha$,则 $\alpha$ 为锐角,且\[\begin{split}\dfrac {PQ}{QR}&=\dfrac {1}{\tan \alpha}=\left|\dfrac {1+k_1k_2}{k_1-k_2}\right|\\&=\dfrac {8+n^2}{2|n|}\geqslant \dfrac {2\sqrt {8\cdot n^2}}{2|n|}\\&=2\sqrt 2,\end{split}\]当 $n=\pm 2\sqrt 2$ 时,$\dfrac {PQ}{QR}$ 取到最小值,为 $2\sqrt 2$.

