每日一题[923]一念之差

已知$f(x)=\ln x-x^3+2{\rm e}x^2-ax$有$2$个零点，求实数$a$的取值范围．

正确答案是$\left(-\infty,{\rm e}^2+{\rm e}^{-1}\right)$．

分离变量法　问题可以转化为函数 $$g(x)=\dfrac{\ln x}x-x^2+2{\rm e}x$$ 的图象与直线$y=a$有两个公共点．而$g(x)$的导函数 $$g'(x)=2\left({\rm e}-x\right)+\dfrac{1-\ln x}x,$$ 于是函数$g(x)$在$(0,{\rm e})$上单调递增，在$({\rm e},+\infty)$上单调递减，在$x={\rm e}$处取得极大值，亦为最大值 $$g({\rm e})={\rm e}^2+{\rm e}^{-1},$$ 考虑到 $$\lim_{x\to 0^+}g(x)=\lim_{x\to +\infty}g(x)=-\infty,$$ 于是$a$的取值范围是$\left(-\infty,{\rm e}^2+{\rm e}^{-1}\right)$．

整体考虑　函数$f(x)$的导函数 $$f'(x)=\dfrac {-3x^3+4{\rm e}x^2+1}x-a,$$ 其极值点$x=x_0$满足 $$-3x_0^3+4{\rm e}x_0^2+1-ax_0=0,$$ 因此对应的极值为 $$f(x_0)=\ln x_0-x_0^3+2{\rm e}x_0^2-ax_0=\ln x_0+2x_0^3-2{\rm e}x_0^2-1.$$ 记 $$\varphi(x)=\ln x+2x^3-2{\rm e}x^2-1,$$ 则其导函数 $$\varphi'(x)=\dfrac{6x^3-4{\rm e}x^2+1}x,x>0$$ 于是函数$\varphi(x)$先单调递增，再单调递减，然后单调递增，不难证明它的极值小于$0$，因此有唯一零点$x={\rm e}$．函数$\varphi(x)$的图象如图．
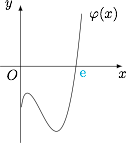考虑函数 $$a(x)=\dfrac {-3x^3+4{\rm e}x^2+1}x,$$ 函数$a(x)$的导函数 $$a'(x)=\dfrac{-6x^3+4{\rm e}x^2-1}{x^2},$$ 因此其图象如图．

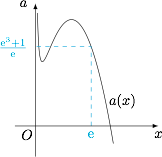这样我们就得到了讨论的分界点$a({\rm e})={\rm e}^2+{\rm e}^{-1}$，分类讨论如下．

情形一　$a>{\rm e}^2+{\rm e}^{-1}$．此时对应的极值点(即$a=a(x)$的解$x_i$)都小于${\rm e}$，因此极值($\varphi(x_i)$)均小于$0$，不符合题意；

情形二　$a={\rm e}^2+{\rm e}^{-1}$．此时对应两个极值点小于${\rm e}$，最大的极值点为${\rm e}$，因此有两个极值小于$0$，极大值亦为最大值为$0$，不符合题意；

情形三　$a<{\rm e}^2+{\rm e}^{-1}$．此时最大的极值点大于${\rm e}$，对应的极大值亦为最大值大于$0$，且其他极值(如果存在的话)均小于$0$，再结合函数的单调性和极限(根据$a$与$a(x)$的大小关系)，可知函数$f(x)$的零点个数为$2$，符合题意．

综上所述，实数$a$的取值范围是$\left(-\infty,{\rm e}^2+{\rm e}^{-1}\right)$．