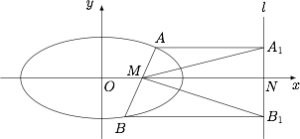
已知椭圆$E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的长轴上一点$M(m,0)$，垂直于$x$轴直线$l$与$x$轴交于点$N\left(\dfrac{a^2}{m},0\right)$．过$M$且斜率不为$0$的直线与椭圆交于$A,B$两点，分别过$A,B$作直线$l$的垂线，垂足为$A_1,B_1$．设$\triangle MAA_1$，$\triangle MBB_1$，$\triangle A_1B_1M$的面积分别为$S_1,S_2,S_3$，求证：$\dfrac{S_1S_2}{S_3^2}$为定值．
分析与解 定值是$\dfrac 14$．
法一 如图，连接$AN,BN,AB_1,BA_1$，设$AB_1$与$MN$交于点$T$．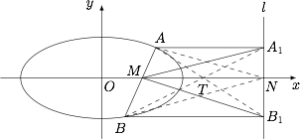
根据椭圆的极点极线性质，有\[\dfrac{AM}{AA_1}=\dfrac{BM}{BB_1},\]因此\[\begin{aligned}MT&=BB_1\cdot \dfrac{AM}{AB}=\dfrac{AA_1\cdot BB_1}{AA_1+BB_1},\\NT&=AA_1\cdot \dfrac{B_1N}{A_1B_1}=AA_1\cdot \dfrac{BM}{AB}=\dfrac{AA_1\cdot BB_1}{AA_1+BB_1},\end{aligned}\]因此$T$点平分$MN$．进而可得$BA_1$与$MN$的交点也平分$MN$，因此$AB_1,A_1B,MN$三线共点．所以\[\begin{split}\dfrac{S_1S_2}{S_3^2}&=\dfrac{AA_1\cdot A_1N\cdot BB_1\cdot B_1N}{\left(MN\cdot A_1B_1\right)^2}\\&=\dfrac 14\cdot \dfrac{AA_1}{TN}\cdot \dfrac{BB_1}{TN}\cdot \dfrac{A_1N\cdot B_1N}{A_1B_1^2}\\&=\dfrac 14\cdot \dfrac{A_1B_1}{B_1N}\cdot \dfrac{A_1B_1}{A_1N}\cdot \dfrac{A_1N\cdot B_1N}{A_1B_1^2}\\&=\dfrac 14,\end{split}\]因此原命题得证．
法二 设直线$AB:x=ty+m$，$A(x_1,y_1)$，$B(x_2,y_2)$．记$n=\dfrac{a^2}{m}$，联立直线$AB$的方程与椭圆方程可得\[\left(b^2t^2+a^2\right)y^2+2b^2tmy+b^2\left(m^2-a^2\right)=0,\]而\[\begin{split}
\dfrac{S_1S_2}{S_3^2}&=\dfrac{-y_1y_2\left(n-x_1\right)\left(n-x_2\right)}{(n-m)^2\left(y_1-y_2\right)^2}\\&=\dfrac{-y_1y_2\left(ty_1+m-n\right)\left(ty_2+m-n\right)}{(n-m)^2\left(y_1-y_2\right)^2}\\&=\dfrac{-y_1y_2\left[t^2y_1y_2-t(n-m)\left(y_1+y_2\right)+(n-m)^2\right]}{(n-m)^2\left[\left(y_1+y_2\right)^2-4y_1y_2\right]}\\&=\dfrac{b^2(a^2-m^2)\left[t^2b^2(m^2-a^2)+t(n-m)\cdot 2b^2tm+(n-m)^2(b^2t^2+a^2)\right]}{(n-m)^2\left[4a^2b^2(b^2t^2+a^2)-4a^2b^2m^2\right]}\\&=\dfrac{a^2-m^2}{4a^2(n-m)^2}\cdot \dfrac{b^2t^2(n^2-a^2)+a^2(n-m)^2}{b^2t^2+a^2-m^2},\end{split}\]而\[(a^2-m^2)(n^2-a^2)=-m^2n^2+a^2(n^2+m^2)-a^4=a^2(n-m)^2,\]因此可得$\dfrac{S_1S_2}{S_3^2}$为定值$\dfrac 14$．