已知$f(x)=\left|x{\rm e}^x\right|$，又$g(x)=f^2(x)-tf(x)$($t\in\mathbb R$)，若满足$g(x)=-1$的$x$有四个，则$t$的取值范围是________．
正确答案是$\left({\rm e}+{\rm e}^{-1},+\infty\right)$．
分析与解 方程$g(x)=-1$，即\[f^2(x)-tf(x)+1=0,\]也即\[t=f(x)+\dfrac{1}{f(x)}.\]考虑复合函数\[y=u+\dfrac 1u,u=\left|x{\rm e}^x\right|,\]以及直线$y=t$．由于函数$u=\left|x{\rm e}^x\right|$的图象如图，因此函数$y=u+\dfrac 1u$的图象和直线$y=t$有两个公共点，且它们的横坐标$u_1,u_2$满足$0<u_1<{\rm e}^{-1}<u_2$．因此对应的$t$的取值范围是$\left({\rm e}+{\rm e}^{-1},+\infty\right)$．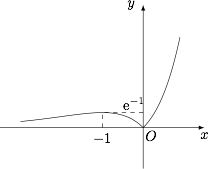
其他方法
令$u=f(x)$，则有$u^2-tu+1=0$，记此方程的两根为$u_1,u_2$，则方程$g(x)=-1$的根即$u_i=f(x),i=1,2$的根．画出$u=f(x)$的图象：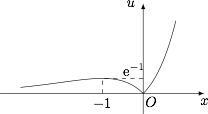
结合图象知$u_i=f(x),i=1,2$有四个根时有$$u_1\in(0,{\rm e}^{-1}),u_2\in({\rm e}^{-1},+\infty),$$即一元二次方程$u^2-tu+1=0$的两根分别在区间$(0,{\rm e}^{-1}),({\rm e}^{-1},+\infty)$上．
记$g(x)=x^2-tx+1$，因为$g(0)=1>0$，所以$g({\rm e}^{-1})<0$即可，解得$t>{\rm e}+{\rm e}^{-1}$．