已知$a,b\in \mathbb R$且$0\leqslant a+b\leqslant 1$,函数$f(x)=x^2+ax+b$在区间$\left[-\dfrac 12,0\right]$上至少存在一个零点,求$a-2b$的取值范围.
分析与解 如图,考虑到$f(1)=1+a+b$,而\[f\left(-\dfrac 12\right)=\dfrac 14-\dfrac 12(a-2b),\]因此问题可以转化为函数$y=x^2+ax+b$的图象和线段$AB$和线段$OC$都有公共点,求$f\left(-\dfrac 12\right)$的取值范围,其中$A(1,1)$,$B(1,2)$,$C\left(-\dfrac 12,0\right)$.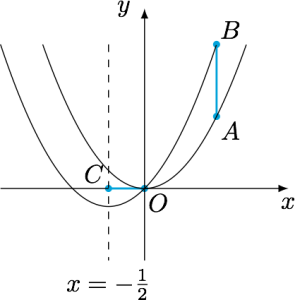
由图可知$f\left(-\dfrac 12\right)$的取值范围是$\left[-\dfrac 14,\dfrac 14\right]$,因此可得$a-2b$的取值范围是$[0,1]$,证明如下.
首先,当$(a,b)=(1,0)$时,$f(0)=0$,此时$a-2b=1$;当$(a,b)=(0,0)$时,$f(0)=0$,此时$a-2b=0$.结合连续性可知$a-2b$可以取遍$[0,1]$内的所有实数;
其次,若$a-2b>1$,则$a-2b>a+b$,从而$b<0$,进而$a>0$.此时\[\begin{aligned}
f\left(-\dfrac 12\right)&=\dfrac 14-\dfrac 12(a-2b)<0,\\f(0)&=b<0,\end{aligned}\]因此函数$f(x)$在$\left[-\dfrac 12,0\right]$上没有零点,不符合题意;
最后,若$a-2b<0$,则$a-2b<a+b$,从而$b>0$,$a<1$,此时$f(x)$的判别式\[\Delta=a^2-4b,\]当$a>0$时,有$a^2<a$,所以$\Delta <a-4b<a-2b<0$,函数$f(x)$在$\left[-\dfrac 12,0\right]$上没有零点,不符合题意.
当$a\leqslant 0$时,$f(x)$的对称轴$x=-\dfrac a2\geqslant 0$,又$f(0)=b>0$,所以$f(x)$在$\left[-\dfrac 12,0\right]$上没有零点,不符合题意.
综上所述,$a-2b$的取值范围是$[0,1]$.
其他方法 设$a+b=3m,a-2b=3n$,则有$\begin{cases} a=2m+n,\\b=m-n\end{cases}$,于是问题转化为函数$$f(x)=x^2+(2m+n)x+(m-n)$$在$x\in\left[-\dfrac 12,0\right]$上有零点,$m\in\left[0,\dfrac 13\right]$,求$3n$的取值范围.
将参数$n$分离得到$$n=\dfrac {x^2+2mx+m}{1-x}=\dfrac {x^2}{1-x}+\dfrac {2x+1}{1-x}\cdot m,$$求右边函数的值域:
先将右边看成以$x\in\left[-\dfrac 12,0\right]$为参数的,关于$m$的函数,记为$g(m)$,因为$\dfrac {2x+1}{1-x}\geqslant 0$,所以$g(m)$的最小值为$g(0)=\dfrac {x^2}{1-x}$,最大值为$g\left(\dfrac 13\right)=\dfrac {3x^2+2x+1}{3(1-x)}$.从而有$$n\in\left[\dfrac {x^2}{1-x},\dfrac {3x^2+2x+1}{3(1-x)}\right],$$令$t=1-x\in\left[1,\dfrac 32\right]$,则有$$y=\dfrac {x^2}{1-x}=t+\dfrac 1t-2\in\left[0,\dfrac 16\right],$$而$$y=\dfrac {3x^2+2x+1}{3(1-x)}=\dfrac{3(t-1)^2+2(1-t)+1}{3t}=t+\dfrac 2t-\dfrac 83\in\left[2\sqrt 2-\dfrac 83,\dfrac 13\right],$$所以$n\in\left[0,\dfrac 13\right]$,从而$a-2b=3n\in[0,1]$.

