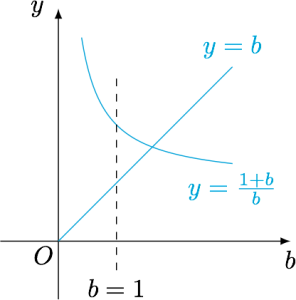设$\triangle ABC$的三边长分别为$a,b,c$,且$a\leqslant b\leqslant c$,定义$\triangle ABC$的倾斜度\[t=\max\left\{\dfrac ab,\dfrac bc,\dfrac ca\right\}\cdot \min\left\{\dfrac ab,\dfrac bc,\dfrac ca\right\}.\]
(1) 若$\triangle ABC$为等腰三角形,求$\triangle ABC$的倾斜度;
(2) 若$a=1$,求$t$的取值范围.
正确答案是(1) $1$;(2) $\left[1,\dfrac{1+\sqrt 5}2\right)$.
分析与解 (1)若$\triangle ABC$为等腰三角形,先设三边分别为$x,x,y,x\leqslant y$,则\[t=\max\left\{1,\dfrac xy,\dfrac yx\right\}\cdot \min\left\{1,\dfrac xy,\dfrac yx\right\}=\dfrac yx\cdot\dfrac xy=1.\]若三边分别为$x,y,y,x\leqslant y$,则\[t=\max\left\{\dfrac xy,1,\dfrac yx\right\}\cdot \min\left\{\dfrac xy,1,\dfrac yx\right\}=1.\]
(2) 若$a=1$,则\[t=\max\left\{\dfrac 1b,\dfrac bc,c\right\} \cdot \min\left\{\dfrac 1b,\dfrac bc,c\right\},\]考虑三者两两相等,得到关于$c$的讨论分界点为$\dfrac 1b,\sqrt b,b^2$.考虑到$1\leqslant b\leqslant c$,最终得到的讨论分界点为$b^2$.
情形一 $b\leqslant c < b^2$.此时\[t=c\cdot \dfrac 1b=\dfrac cb,\]考虑到$c<1+b$,于是\[1\leqslant t<\min \left\{b,\dfrac 1b+1\right\}=\dfrac{1+\sqrt 5}2.\]
情形二 $c\geqslant b^2$.此时\[t=c\cdot \dfrac bc=b,\]考虑到$c<1+b$,于是\[t+1>t^2,\]解得\[1\leqslant t<\dfrac{1+\sqrt 5}2.\]
综上所述,$t$的取值范围是$\left[1,\dfrac{1+\sqrt 5}2\right)$.
其他方法 由题意知$\dfrac ab\leqslant 1,\dfrac bc\leqslant 1,\dfrac ca\geqslant 1$,所以$$t=\dfrac ca\cdot\min\left\{\dfrac ab,\dfrac bc\right\}=\min\left\{\dfrac ca\cdot\dfrac ab,\dfrac ca\cdot\dfrac bc\right\}=\min\left\{\dfrac cb,\dfrac ba\right\}\geqslant 1.$$
(1)由题意知$a=b$或$b=c$,所以$t=1$;
(2)$a=1$时,$t=\min\left\{\dfrac cb,b\right\}$,而$1\leqslant b\leqslant c< 1+b$,所以$t<\min\left\{\dfrac {1+b}b,b\right\}$.
记$f(b)=\min\left\{\dfrac {1+b}b,b\right\}$,在坐标系$bOy$中画出函数$y=\dfrac {1+b}{b},y=b$的图象:
当$\dfrac {1+b}{b}=b$,即$b=\dfrac {1+\sqrt 5}{2}$时,$f(b)$有最大值$b=\dfrac {1+\sqrt 5}{2}$,所以$t\in\left[1,\dfrac {1+\sqrt 5}{2}\right)$.