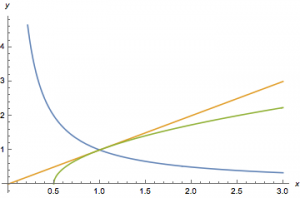
已知\(a>0\)，\(a^2-2ab+c^2=0\)，\(bc>a^2\)，试比较\(a,b,c\)的大小．
根据题意，有\[\begin{cases}1-2\cdot\dfrac ba+\left(\dfrac ca\right)^2=0\\\dfrac ba\cdot\dfrac ca>1\end{cases}\]
令\(\dfrac ba=x\)，\(\dfrac ca=y\)，则\(y^2-2x+1=0\)且\(xy>1\)．
由于\(b=\dfrac{a^2+c^2}{2a}>0\)，由\(bc>a^2>0\)，于是\(x,y>0\)．
用规划方法，可得\(x>y>1\)，于是\(b>c>a\)．
