已知函数\(f(x)=2x-\dfrac{x^2}{\pi}+\cos x\).设\(x_1,x_2\in (0,\pi)\),\(x_1\neq x_2\)且\(f(x_1)=f(x_2)\).若\(x_1,x_0,x_2\)成等差数列,则( )
A.\(f'(x_0)<0\)
B.\(f'(x_0)=0\)
C.\(f'(x_0)>0\)
D.\(f'(x_0)\)的符号不确定
考虑到\[f'(x_0)=f'\left(\dfrac{x_1+x_2}{2}\right)=2-\dfrac{x_1+x_2}{\pi}-\sin\dfrac{x_1+x_2}{2},\]
而根据题意有\[2x_1-\dfrac{x_1^2}{\pi}+\cos x_1=2x_2-\dfrac{x_2^2}{\pi}+\cos x_2,\]于是\[\begin{split}2-\dfrac{x_1+x_2}{\pi}&=-\dfrac{\cos x_1-\cos x_2}{x_1-x_2}\\&=\dfrac{\sin\dfrac{x_1-x_2}2}{\dfrac{x_1-x_2}2}\cdot\sin\dfrac{x_1+x_2}{2}\\&<\sin\dfrac{x_1+x_2}{2},\end{split}\]
因此可得\(f'(x_0)<0\),选A.最后附上该函数的图象.
2015年1月21日补充改编题:
已知$f(x)=x^2+ax+\sin\dfrac{\pi}2x$,$x\in (0,1)$.
(1)若$f(x)$在$(0,1)$上是单调递增函数,求$a$的取值范围.
(2)当$a=-2$时,$f(x)\geqslant f(x_0)$恒成立,$f(x_1)=f(x_2)$,求证:$x_1+x_2\geqslant 2x_0$.
答案 (1)$\left[-\dfrac{\pi}{2},+\infty\right)$;(2)略.
提示 (2)当$x_1=x_2$时,命题不难证明;当$x_1\neq x_2$时,由$f(x_1)=f(x_2)$可以整理得$$(x_1+x_2)-2+\dfrac{\pi}{2}\cos\dfrac{\pi(x_1+x_2)}4>0,$$进而可得$\dfrac{x_1+x_2}2>x_0$.


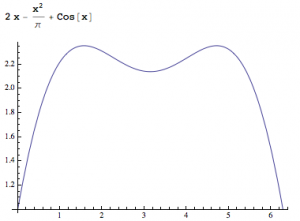
\(f(x_1)=f(x_2)\)
每日一题要第二天公布答案好不?这样同学们可以在评论里答题的好不?
PS:评论里可以使用\(\latex\)嘛?