每日一题[843]瓮中捉鳖

已知$x_1\ln x_1=x_2\ln x_2$，且$x_1<x_2$，若整数$k=\dfrac 52\left(x_1+x_2+2\sqrt{x_1x_2}\right)$，求$k$的值．

正确答案是$3$．

分析与解　问题即函数$y=x^2\ln x$与$y=a$的两个公共点的横坐标设为$x_1,x_2$，估计$x_1+x_2$的范围．事实上，我们有 $$1<x_1+x_2<\dfrac{2}{\sqrt{\rm e}}.$$ 下面进行证明：

由于$f(x)=x^2\ln x$的导函数 $$f'(x)=x(1+2\ln x),$$ 于是函数$f(x)$在$x=\dfrac{1}{\sqrt{\rm e}}$处取得极小值，如图．

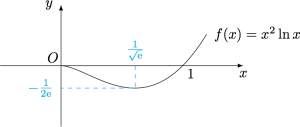容易知道$0<x_1<\dfrac{1}{\sqrt{\rm e}}<x_2<1$，只需要证明 $$1-x_1<x_2<\dfrac{2}{\sqrt {\rm e}}-x_1,$$ 可以转化为证明 $$\begin{cases}\forall x\in\left(0,\dfrac 12\right),f(x)>f(1-x),\\ \forall x\in \left(0,\dfrac{1}{\sqrt{\rm e}}\right),f(x)<f\left(\dfrac{2}{\sqrt {\rm e}}-x\right).\end{cases}$$ 设$\varphi(x)=f(x)-f(1-x)$，$\mu(x)=f(x)-f\left(\dfrac{2}{\sqrt {\rm e}}-x\right)$，则 $$\begin{aligned}\varphi'(x)&=f'(x)+f'(1-x)=2x\ln x+2(1-x)\ln (1-x)+1,\\\varphi''(x)&=f''(x)-f''(1-x)=2\ln x-2\ln(1-x),\end{aligned}$$ 在$\left(0,\dfrac 12\right)$上，$\varphi'(x)$单调递减，结合$\varphi'\left(\dfrac 12\right)<0$，$\lim\limits_{x\to 0^+}{\varphi'(x)}=1$，于是$\varphi(x)$在$\left(0,\dfrac 12\right)$上先单调递增，后单调递减，结合 $$\lim\limits_{x\to 0^+}\varphi(x)=\varphi\left(\dfrac 12\right)=0,$$ 可得当$x\in\left(0,\dfrac 12\right)$时，$\varphi(x)>0$．而 $$\begin{aligned}\mu'(x)&=f'(x)+f'\left(\dfrac{2}{\sqrt{\rm e}}-x\right)=\dfrac{2}{\sqrt{\rm e}}+x\ln x+\left(\dfrac{2}{\sqrt {\rm e}}-x\right)\ln \left(\dfrac{2}{\sqrt {\rm e}}-x\right) , \\\mu''(x)&=f''(x)-f''\left(\dfrac{2}{\sqrt {\rm e}}-x\right)=2\ln x-2\ln\left(\dfrac{2}{\sqrt{\rm e}}-x\right),\end{aligned}$$ 于是$\mu'(x)$在$\left(0,\dfrac{1}{\sqrt {\rm e}}\right)$上单调递减，结合$\mu'\left(\dfrac{1}{\sqrt{\rm e}}\right)>0$，可得当$x\in\left(0,\dfrac{1}{\sqrt{\rm e }}\right)$时，$\mu'(x)>0$，$\mu(x)$单调递增，结合$\mu\left(\dfrac{1}{\sqrt{\rm e}}\right)=0$，可得当$x\in\left(0,\dfrac{1}{\sqrt{\rm e}}\right)$时，$\mu(x)<0$．

综上所述，我们得到了 $$k=\dfrac 52(x_1+x_2)^2$$ 的范围是$\left(\dfrac 52,\dfrac{10}{\rm e}\right)$，于是$k$的值为$3$．