已知抛物线$C:y^2=4x$的焦点为$F$，直线$MN$过焦点$F$且与抛物线$C$交于$M,N$两点，$P$为抛物线$C$准线$l$上一点，且$PF\perp MN$．连结$PM$交$y$轴于$Q$点，过$Q$作$QD\perp MF$于点$D$，若$|MD|=2|FN|$，求$|MF|$．
正确答案是$2+\sqrt 3$．
分析与解 如图．
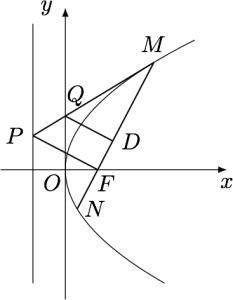设$M(4m^2,4m)$，$N(4n^2,4n)$，则根据抛物线的平均性质，有\[4m^2\cdot 4n^2=1.\]根据题意，有\[\dfrac{|MD|}{|FN|}=\dfrac{|MQ|}{|MP|}\cdot \dfrac{|MF|}{|FN|}=\dfrac{4m^2}{4m^2+1}\cdot \dfrac{4m^2+1}{4n^2+1}=\dfrac{4m^2}{4n^2+1}=2,\]于是可得\[2m^2=4n^2+1,\]将$4n^2=\dfrac{1}{4m^2}$代入，可得\[2m^2=\dfrac{1}{4m^2}+1,\]即\[8m^4-4m^2-1=0,\]解得$m^2=\dfrac{1+\sqrt{3}}{4}$，因此\[|MF|=4m^2+1=2+\sqrt 3.\]