每日一题[90] 构造函数估计对数值

2014年高考湖北卷理科数学第22题、文科数学第21题： 将${\mathrm e}^3$，$3^{\mathrm e}$，$\pi^{\mathrm e}$，${\mathrm e}^\pi$，$3^\pi$，$\pi^3$从小到大排列．

首先由同底数及同指数幂的比较方法可得 $$3^{\mathrm e}<{\pi}^{\mathrm e}<{\pi}^3.$$ 考虑到比较$a^b$与$b^a$的大小关系即比较$\dfrac{\ln a}{a}$与$\dfrac{\ln b}{b}$的大小关系，因此构造辅助函数$f(x)=\dfrac{\ln x}{x}$． 如图为函数$f(x)=\dfrac{\ln x}{x}$的图象，它在$(0,{\mathrm e})$上单调递增，在$({\mathrm e},+\infty)$上单调递减，在$x={\mathrm e}$处取得最大值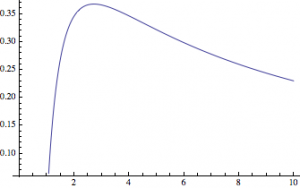． 于是我们有 $$\dfrac{1}{\mathrm e}>\dfrac{\ln 3}{3}>\dfrac{\ln \pi}{\pi},$$ 于是可得 $${\mathrm e}^3>3^{\mathrm e}\land {\mathrm e}^\pi >{\pi}^{\mathrm e}\land 3^{\pi}>{\pi}^3,$$ 结合之前已经得到的大小关系，可以画数轴如下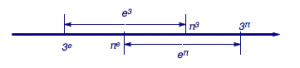： 接下来的任务就是比较${\mathrm e}^3$与${\pi}^{\mathrm e}$的大小关系以及${\mathrm e}^{\pi}$与${\pi}^3$的大小关系．与之前的手段类似，就是比较$\ln{\pi}$与$\dfrac{3}{\mathrm e}$以及$\dfrac{\pi}{3}$的大小关系．考虑到 $$\dfrac{3}{\mathrm e}=1.10...$$ 以及 $$\dfrac{\pi}{3}=1.04...$$ 因此问题的关键在于如何估计$\ln{\pi}$的大小． 为了引入$\pi$而不将$3$卷入其中，考虑 $$\dfrac{{\mathrm e}^2}{\pi}<\mathrm e,$$ 于是 $$\dfrac{\ln \dfrac{{\mathrm e}^2}{\pi}}{\dfrac{{\mathrm e}^2}{\pi}}<\dfrac{1}{\mathrm e},$$ 即 $$\ln{\pi}>2-\dfrac{\mathrm e}{\pi}>1.12,$$ 因此 $$\ln{\pi}>\dfrac{3}{\mathrm e}\land \ln{\pi}> \dfrac{\pi}{3},$$ 进而 $${\mathrm e}^3<{\pi}^{\mathrm e}\land {\mathrm e}^{\pi}<{\pi}^3,$$ 因此 $$3^{\mathrm e}<{\mathrm e}^3<{\pi}^{\mathrm e}<{\mathrm e}^{\pi}<{\pi}^3<3^{\pi}.$$