如图，两个正三角形$ABC,A_1B_1C_1$组成“六芒星”，$O$为“六芒星”的中心，$P$为“六芒星”图案上一点(边界上)，且$\overrightarrow {OP}=x\overrightarrow {OD}+y\overrightarrow {OC_1}$，则$x+y$的取值范围是________．
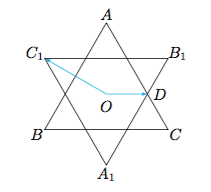
正确答案是$[-5,5]$．
分析与解 连结$C_1D,AA_1$，并记它们的交点为$N$，记$B_1C_1$的中点为$M$，如下图：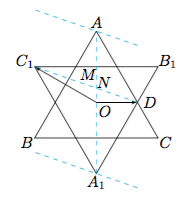
由向量的等系数和线知当点$P$在直线$C_1D$上时，有$x+y=1$；
作一系列与$C_1D$平行的直线与六芒星图案相交，并与线段$AA_1$相交于一点，记为$Q$，则$x+y$的绝对值为$OQ$与$ON$长度的比值，从而当点$P$与$A,A_1$重合时，$x+y$分别取到最大值与最小值，下面计算$OA:ON$的值：
一方面$ON:MN=OD:C_1M=2:3$，所以$ON=\dfrac 25OM$；
另一方面，$AM=MO$，所以$ON=\dfrac 15OA$．
从而得到$x+y\in[-5,5]$．