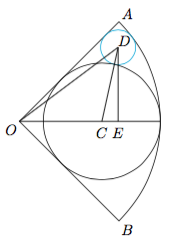
已知扇形$OAB$中,$\angle AOB$为直角,圆$C$与$OA,OB$及圆$O$相切,圆$D$与$OA$,圆$O$,圆$C$相切.作$DE\perp OC$,垂足为$E$.求证:$\triangle ODE$的三边成等差数列.

分析与解 不妨设$OA=\sqrt 2+1$,$OC=\sqrt 2$,则圆$D$的半径$$r=\sqrt 2+1-DO=DC-1,$$于是$DO+DC=\sqrt 2+2$,因此$D$在以$O,C$为焦点,$\sqrt 2+2$为长轴长的椭圆上.设$\angle DOC=\theta$,则由焦半径公式得$$OD=\dfrac{\left(\dfrac{\sqrt 2+2}2\right)^2-\left(\dfrac{\sqrt 2}2\right)^2}{\dfrac{\sqrt 2+2}2-\dfrac{\sqrt 2}2\cdot \cos\theta}=\dfrac{\sqrt 2+2}{\sqrt 2+1-\cos\theta}.$$因此有$$r=OD\cdot \sin\left(\dfrac{\pi}4-\theta\right)=\sqrt 2+1-OD,$$即$$\dfrac{\sqrt 2+2}{\sqrt 2+1-\cos\theta}\cdot \dfrac{\sqrt 2}2\left(\cos\theta-\sin\theta\right)=\sqrt 2+1-\dfrac{\sqrt 2+2}{\sqrt 2+1-\cos\theta},$$整理可得$$2\cos\theta-\sin\theta=1,$$于是$\sin\theta=\dfrac 35$,因此原命题得证.