(2013年全国I卷)如图，在$\triangle ABC$中，$\angle ABC=90^\circ$，$AB=\sqrt 3$，$BC=1$，$P$为$\triangle ABC$内一点，$\angle BPC=90^\circ$．
(1) 若$PB=\dfrac 12$，求$PA$；
(2) 若$\angle APB=150^\circ$，求$\tan \angle PBA$．
分析与解 三角方法
(1) 由$PB=\dfrac 12$，可得$\angle PBC=60^\circ$，于是$\angle PBA=30^\circ$，在$\triangle PAB$中应用余弦定理，可得$$PA^2=PB^2+AB^2-2PB\cdot AB\cdot \cos\angle PBA=\dfrac 74,$$于是$PA=\dfrac{\sqrt 7}2$．
(2) 设$\angle PBA=x$，则$\angle PCB=x$，于是$PB=\sin x$，在$\triangle PAB$中应用正弦定理，可得$$\dfrac{AB}{\sin\angle APB}=\dfrac{PB}{\sin\angle PAB},$$即$$\dfrac{\sqrt 3}{\sin 150^\circ}=\dfrac{\sin x}{\sin(30^\circ -x)},$$整理得$$\sqrt 3\cos x=4\sin x,$$于是所求正切值$\tan x=\dfrac{\sqrt 3}4$．
解析方法 如图建立平面直角坐标系．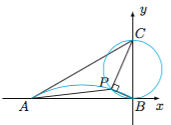
(1) 以$BC$为直径的圆的方程为$$x^2+\left(y-\dfrac 12\right)^2=\dfrac 14,$$即$x^2+y^2-y=0$，设$P(m,n)$($m<0$)，则$$\begin{cases} m^2+n^2=\dfrac 14,\\m^2+n^2-n=0,\end{cases} $$解得$m=-\dfrac{\sqrt 3}4,n=\dfrac 14$．于是$PA=\sqrt{(m+\sqrt 3)^2+n^2}=\dfrac{\sqrt 7}2$．
(2) 过点$A,P,B$的圆的方程为$\left(x+\dfrac{\sqrt 3}2\right)^2+\left(y+\dfrac 32\right)^2=3$，即$x^2+y^2+\sqrt 3x+3y=0$．该圆与以$BC$为直径的圆的公共弦$PB$所在的直线方程为$$\left(x^2+y^2-y\right)-\left(x^2+y^2+\sqrt 3x+3y\right)=0,$$也即$$\sqrt 3x+4y=0,$$于是所求的正切值为$\dfrac{\sqrt 3}4$．