已知$x>0$，考虑方程$a^x=x^a$，其中$a>0$且$a\ne 1$．
(1) 若方程只有一个实数解，求$a$的取值范围；
(2) 若方程有两个实数解$x_1,x_2$，求证：$x_1+x_2>2{\rm e}$．
分析与解 (1) 方程$a^x=x^a$等价于$$\dfrac{\ln x}{x}=\dfrac{\ln a}{a},$$记$f(x)=\dfrac {\ln x}x$，则$$f'(x)=\dfrac {1-\ln x}{x^2},$$于是$f(x)$草图如下：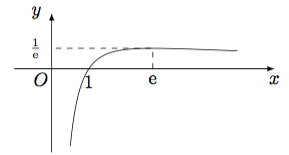
于是当$a={\rm e}$或$0<a<1$时方程只有一个实数解．因此$a$的取值范围是$(0,1)\cup\left\{ {\rm e}\right\}$．
(2) 根据第(1)小题，可得$\dfrac{\ln a}a\in \left(0,\dfrac{1}{\rm e}\right)$．由于$$\begin{cases} a\ln x_1=x_1\ln a,\\ a\ln x_2=x_2\ln a,\end{cases} $$于是$$a\left(\ln x_1-\ln x_2\right)=(x_1-x_2)\ln a,$$从而根据对数平均不等式$$\dfrac{x_1+x_2}2>\dfrac{x_1-x_2}{\ln x_1-\ln x_2}=\dfrac{a}{\ln a}>{\rm e},$$原命题得证．
注 不妨设$x_1<x_2$，第二问也可以直接证明$x_2>2{\mathrm e}-x_1$成立，由$f(x)$的单调性知，这等价于证明$f(x_2)<f(2{\mathrm e}-x_1)$，而$f(x_2)=f(x_1)$，且$x_1\in(0,\mathrm e)$，所以只需要证明$f(x)-f({2\mathrm e}-x)<0$对$x\in(0,{\mathrm e})$恒成立即可．而这等价于$$\forall x\in(0,\mathrm e),({2\mathrm e}-x)\ln x-x\ln({2\mathrm e}-x)<0,$$记左边为函数$g(x)$，则有$$g'(x)=\dfrac {(2{\mathrm e}-x)^2+x^2}{x(2{\mathrm e}-x)}-\ln[x(2{\mathrm e}-x)]>0,$$而$g(\mathrm e)=0$，于是不等式得证．