在$\triangle ABC$中，$M$是$BC$的中点，$BM=2$，$AM=AB-AC$，则$\triangle ABC$的面积的最大值为_______．
正确答案是$2\sqrt 3$．
分析与解 以$BC$所在直线为$x$轴，以$M$为坐标原点建立平面直角坐标系，$\triangle ABC$的面积只与$A$点的纵坐标相关．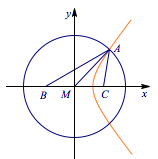
设$AM$的长为$2a$，则点$A$既在以$M$为圆心，$2a$为半径的圆上，也在以$B,C$为焦点，实轴长为$2a$的双曲线右支上，联立圆与双曲线的方程有$$\begin{cases} \dfrac {x^2}{a^2}+\dfrac {y^2}{a^2}=4,\\\dfrac {x^2}{a^2}-\dfrac {y^2}{4-a^2}=1,\end{cases}$$两式相减得$$y^2=\dfrac 34a^2(4-a^2)\leqslant 3,$$当且仅当$a=\sqrt 2$时取到等号，所以$$\left(S_{\triangle ABC}\right)_{\max}=\dfrac 12\cdot 4\cdot \sqrt 3=2\sqrt 3.$$