每日一题[733]紧密相连

设函数$f(x)={\rm e}^x-ax+a$($a\in\mathbf R$)，其图象与$x$轴交于$A(x_1,0)$，$B(x_2,0)$两点，且$x_1<x_2$．
(1) 求$a$的取值范围；
(2) 求证：$f'\left(\sqrt{x_1x_2}\right)<0$；
(3) 设$C$在函数$y=f(x)$的图象上，且$\triangle ABC$为等腰直角三角形，记$\sqrt{\dfrac{x_2-1}{x_1-1}}=t$，求$(a-1)(t-1)$的值．

分析与解　(1) 函数$f(x)$的导函数$$f'(x)={\rm e}^x-a,$$显然有$a>0$，于是在$(-\infty,\ln a)$上函数$f(x)$单调递减，在$(\ln a,+\infty)$上函数$f(x)$单调递增，当$x=\ln a$时函数$f(x)$取得极小值，亦为最小值$$f\left(\ln a\right)=a\left(2-\ln a\right),$$由最小值小于零得到$a$的取值范围是$\left({\rm e}^2,+\infty\right)$．

(2) 由题意，有$$\begin{cases} {\rm e}^{x_1}-ax_1+a=0,\\ {\rm e}^{x_2}-ax_2+a=0,\end{cases} $$于是$$a=\dfrac{{\rm e}^{x_2}-{\rm e}^{x_1}}{x_2-x_1}.$$因此欲证明不等式即$${\rm e}^{\sqrt{x_1x_2}}-\dfrac{{\rm e}^{x_2}-{\rm e}^{x_1}}{x_2-x_1}<0.$$由对数平均不等式以及均值不等式，我们知道$$\dfrac{{\rm e}^{x_2}-{\rm e}^{x_1}}{x_2-x_1}=\dfrac{{\rm e}^{x_2}-{\rm e}^{x_1}}{\ln {\rm e}^{x_2}-\ln {\rm e}^{x_1}}>\sqrt{{\rm e}^{x_1}\cdot{\rm e}^{x_2}}={\rm e}^{\frac{x_1+x_2}2}>{\rm e}^{\sqrt{x_1x_2}},$$因此原命题得证．

(3) 如图，根据题意，$C$的横坐标为$\dfrac{x_1+x_2}2$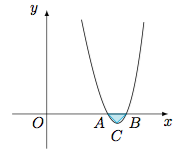．于是$$f\left(\dfrac{x_1+x_2}2\right)=\dfrac{x_1-x_2}2,$$即$${\rm e}^{\frac{x_1+x_2}2}-a\cdot \dfrac{x_1+x_2}2+a+\dfrac{x_2-x_1}2=0.$$又$${\rm e}^{\frac{x_1+x_2}2}=\sqrt{{\rm e}^{x_1}\cdot {\rm e}^{x_2}}=a\sqrt{\left(x_1-1\right)\left(x_2-1\right)}=at\left(x_1-1\right),$$代入，并整理得$$at\left(x_1-1\right)-\dfrac {a+1}2\left(x_1-1\right)-\dfrac {a-1}2\left(x_2-1\right)=0,$$因此$$at-\dfrac{a+1}2-\dfrac{a-1}2t^2=0,$$也即$$\left(t^2-2t+1\right)a=t^2-1,$$于是$$(a-1)(t-1)=2,$$原命题得证．

注　第二问也可以不用对数平均不等式，直接证明$$\dfrac{{\rm e}^{x_2}-{\rm e}^{x_1}}{x_2-x_1}>{\rm e}^{\frac{x_1+x_1}{2}},$$对此式变形得$${\rm e}^{\frac{x_2-x_1}{2}}-{\rm e}^{\frac{x_1-x_2}{2}}>x_2-x_1.$$令$t=\dfrac {x_2-x_1}{2}$，则需要证明的不等式为$${\rm e}^t-{\rm e}^{-t}-2t>0,t>0$$将左边看成关于$t$的函数直接求导便可证明此不等式．