每日一题[746]函数与方程间的转化

若存在实数$m,n$使函数$f(x)=\sqrt{x+3}+k$的定义域为$[m,n]$，值域为$[-n,-m]$，则实数$k$的取值范围是_______．

---

分析与解　$\left[2,\dfrac 94\right)$．

题意即$f(x)$得图象过点$A(m,-n)$，$B(n,-m)$，而$AB:y=x-(m+n)$，于是关于$x$的方程

$$\sqrt{x+3}+k=x-(m+n)$$ 即 $$x+3=x^2-2(m+n+k)x+(m+n+k)^2$$ 有两个实数解$m,n$，从而由韦达定理可得 $$2(m+n+k)+1=m+n,$$ 于是$m+n=-2k-1$．考虑直线$y=x-(m+n)-k$与$y=\sqrt{x+3}$的位置关系，可得$-(m+n)-k$的取值范围是$\left[3,\dfrac{13}4\right)$，如图：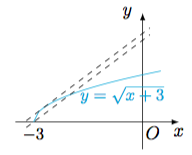

于是$k$的取值范围是$\left[2,\dfrac 94\right)$．

另法　因为$f(x)$为增函数，所以有

$$\begin{cases} \sqrt{m+3}+k=-n,\\\sqrt{n+3}+k=-m,\end{cases}$$ 从而有$-k=\sqrt{m+3}+n=\sqrt{n+3}+m$，于是有 $$m-\sqrt{m+3}=n-\sqrt{n+3}=t,$$ 所以$x-\sqrt{x+3}=t$有两根$m,n$，移项得$\sqrt{x+3}=x-t$，两边平方整理得 $$x^2-(2t+1)x+(t^2-3)=0.$$ 由这个方程的两根为$m,n$及化简过程知$n>m\geqslant -3$，且$n>m\geqslant t$．设 $$g(x)=x^2-(2t+1)x+t^2-3,$$ 则有 $$\begin{cases} \Delta=4t+13 >0,\\g(t)\geqslant 0,\\g(-3)\geqslant 0,\end{cases}$$ 解得$-\dfrac {13}{4}<t\leqslant -3$．

由韦达定理知$m+n=2t+1$，寻找$k$与$t$的关系：

因为

$$\begin{split} 2t=&m+n-\sqrt{m+3}-\sqrt{n+3}\\=&m+n-(-k-n)-(-k-m)\\=&2(m+n+k)\\=&2(2t+1+k),\end{split}$$ 所以$k=-t-1\in\left[2,\dfrac 94\right)$．