每日一题[737]平面向量的几何角度

已知向量$\overrightarrow a,\overrightarrow b,\overrightarrow c$满足$\Big|\overrightarrow  a\Big|=1$，$\Big|\overrightarrow  a-\overrightarrow  b\Big|=\Big|\overrightarrow  b\Big|$，$\left(\overrightarrow  a-\overrightarrow  c\right)\cdot \left(\overrightarrow  b-\overrightarrow  c\right)=0$．对于确定的$\overrightarrow  b$，记$\overrightarrow  c$的长度的最大值和最小值分别为$m,n$，则当$\overrightarrow  b$变化时，$m-n$的最小值是_______．

---

分析与解　$\dfrac 12$．

设$\overrightarrow {OA}=\overrightarrow {a},\overrightarrow {OB}=\overrightarrow {b},\overrightarrow {OC}=\overrightarrow {c}$，则由题意知

$$OA=1,OB=AB,AC\perp BC.$$ 所以点$C$在以$AB$为直径的圆上，记$OA$的中点为$M$，则有$BM\perp OA$，所以点$M$也在以$AB$为直径的圆上，如图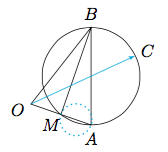：当点$C$在圆上运动时，$m-n=2r=OB$，所以即求$OB$的最小值．当$O,A,B$三点共线时，即$M,B$重合时，$OB$取到最小值$\dfrac 12$．