（2010年广东卷）设$A(x_1,y_1)$，$B(x_2,y_2)$是平面直角坐标系$xOy$上的两点，现定义由点$A$到点$B$的折线距离$d(A,B)=|x_2-x_1|+|y_2-y_1|$．对于平面$xOy$上给定的不同两点$A(x_1,y_1)$，$B(x_2,y_2)$．
(1) 若$C(x,y)$是平面$xOy$上的点，试证明$d(A,C)+d(C,B)\geqslant d(A,B)$；
(2) 在平面$xOy$上是否存在点$C(x,y)$同时满足：$d(A,C)+d(C,B)=d(A,B)$和$d(A,C)=d(C,B)$．若存在，请求出所有符合条件的点；若不存在，请说明理由．
分析与解 (1) 根据题意，有\[\begin{split} LHS&=|x_1-x|+|y_1-y|+|x-x_2|+|y-y_2|\\&\geqslant |(x_1-x)+(x-x_2)|+|(y_1-y)+(y-y_2)|\\&=|x_1-x_2|+|y_1-y_2|=RHS,\end{split} \]因此原命题得证．
(2) 第(1)小题中的不等式取得等号的条件是$$\begin{cases} (x_1-x)(x-x_2)\geqslant 0,\\(y_1-y)(y-y_2)\geqslant 0,\end{cases} $$即$$\begin{cases} \min\{x_1,x_2\}\leqslant x\leqslant \max\{x_1,x_2\},\\\min\{y_1,y_2\}\leqslant y\leqslant \max\{y_1,y_2\},\end{cases} $$因此当$x_1=x_2$或$y_1=y_2$时，$C$为$AB$的中点$M\left(\dfrac{x_1+x_2}2,\dfrac{y_1+y_2}2\right)$；当$x_1\neq x_2$且$y_1\neq y_2$时，点$C$的轨迹是过$AB$的中点$M$，斜率的绝对值为$1$，且与直线$AB$斜率的符号相反的直线被以线段$AB$为对角线各边都与坐标轴方向平行的矩形所截的线段，如图所示．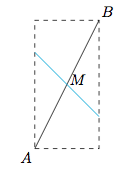 
注 对于条件$d(A,C)=d(C,B)$，即$$|x-x_1|-|x-x_2|+|y-y_1|-|y-y_2|=0.$$因为$x-x_1,x-x_2$符号相反，$y-y_1,y-y_2$的符号也相反，所以点$C$的轨迹是斜率为$1$或$-1$的直线．
若直线$AB$的斜率为正，不妨设$x_1<x_2,y_1<y_2$，则有$$2x+2y-x_1-x_2-y_1-y_2=0,$$即$C$点在斜率为$-1$的直线上，其它情况可同理．
思考与总结 本题中的$d(A,C)+d(C,B)=d(A,B)$可以看成是折线段的定义，$d(A,C)=d(C,B)$可以看成是折线垂直平分线的定义．类似的，我们可以定义折线圆$d(A,C)=r$，折线椭圆$d(A,C)+d(B,C)=2a$，折线双曲线$\left|d(A,C)-d(B,C)\right|=2a$，点到直线的折线距离$\displaystyle d(C,l)=\min_{A\in l}\{d(C,A)\}$，以及折线抛物线$d(C,l)=d(A,C)$．