2011年广东卷高考数学理科第21题（压轴题）：
在平面直角坐标系$xOy$上，给定抛物线$L:y=\dfrac 14x^2$．实数$p,q$满足$p^2-4q\geqslant 0$，$x_1,x_2$是方程$x^2-px+q=0$的两根，记$\varphi(p,q)=\max\{|x_1|,|x_2|\}$．
(1) 过点$A\left(p_0,\dfrac 14p_0^2\right)$($p_0\neq 0$)作$L$的切线交$y$轴于点$B$．证明：对线段$AB$上的任一点$Q(p,q)$，有$\varphi(p,q)=\dfrac 12|p_0|$；
(2) 设$M(a,b)$是定点，其中$a,b$满足$a^2-4b>0$，$a\neq 0$．过$M(a,b)$作$L$的两条切线$l_1,l_2$，切点分别为$E\left(p_1,\dfrac 14p_1^2\right)$，$E'\left(p_2,\dfrac 14p_2^2\right)$，$l_1,l_2$与$y$轴分别交于$F,F'$．线段$EF$上异于两端点的点集记为$X$．证明：$M(a,b)\in X\Leftrightarrow |p_1|>|p_2|\Leftrightarrow \varphi(a,b)=\dfrac 12|p_1|$；
(3) 记$D=\left\{(x,y)\mid y\leqslant x-1,y\geqslant \dfrac 14(x+1)^2-\dfrac 54\right\}$，当$(p,q)$取遍$D$时，求$\varphi(p,q)$的最小值(记为$\varphi_{\min}$)和最大值(记为$\varphi_{\max}$)．
分析与解 (1)法一 显然$A\left(p_0,\dfrac 14p_0^2\right)$在抛物线$L$上，于是过点$A$的抛物线$L$的切线方程为$$y=\dfrac 12p_0x-\dfrac 14p_0^2,$$若$p_0>0$，则线段$AB$的方程为$$y=\dfrac 12p_0x-\dfrac 14p_0^2,0\leqslant x\leqslant p_0,$$若$p_0<0$，则线段$AB$的方程为$$y=\dfrac 12p_0x-\dfrac 14p_0^2,p_0\leqslant x\leqslant 0.$$又若$p^2-4q\geqslant 0$，则方程$x^2-px+q=0$的两根为$\dfrac{p\pm\sqrt{p^2-4q}}{2}$，若$Q(p,q)$在线段$AB$上，则$$q=\dfrac 12p_0p-\dfrac 14p_0^2,$$从而$p^2-4q=\left(p-p_0\right)^2$，从而两根为$$x_{1,2}=\dfrac{p\pm \left|p-p_0\right|}{2}.$$当$p_0>0$时，$0\leqslant p\leqslant p_0$，则$$\varphi(p,q)=\max\{|x_1|,|x_2|\}=\dfrac{p_0}2=\dfrac{|p_0|}2;$$当$p_0<0$时，$p_0\leqslant p\leqslant 0$，则$$\varphi(p,q)=\max\{|x_1|,|x_2|\}=\dfrac{-p_0}2=\dfrac{|p_0|}2.$$因此原命题得证．
法二 过点$A$的抛物线$L$的切线方程为$$y=\dfrac 12p_0x-\dfrac 14p_0^2,$$于是有$q=\dfrac 12p_0p-\dfrac 14p_0^2$，从而考虑方程$x^2-px+\dfrac 12p_0p-\dfrac 14p_0^2=0$的两根即可．
记方程左边为$f(x)$，则有$$f\left(\dfrac 12p_0\right)=0,f\left(-\dfrac 12p_0\right)=p_0p>0.$$所以方程的一根为$\dfrac 12p_0$，另一根$x'\in\left(-\dfrac 12|p_0|,\dfrac 12|p_0|\right)$，从而知$\varphi(p,q)=\dfrac 12|p_0|$．
(2) 由题意知$l_1,l_2$的方程分别为$$l_1:y=\dfrac 12p_1x-\dfrac 14p_1^2,l_2:y=\dfrac 12p_2x-\dfrac 14p_2^2,$$联立解得点$M$的坐标为$(a,b)=\left(\dfrac {p_1+p_2}{2},\dfrac {p_1p_2}{4}\right)$．从而考虑方程$$x^2-\dfrac {p_1+p_2}{2}x+\dfrac {p_1p_2}{4}=0,$$它的两根为$\dfrac 12p_1,\dfrac 12p_2$，所以$\varphi(a,b)=\dfrac 12\max\{|p_1|,|p_2|\}$．
由此知$|p_1|>|p_2|$等价于$\varphi(a,b)=\dfrac 12|p_1|$．下面证明当$M(a,b)\in X$与它们等价：
由(1)知$M(a,b)\in X$时，$\varphi(a,b)=\dfrac 12|p_1|$；
若$|p_1|>|p_2|$，有$$|a|\leqslant \dfrac{|p_1|+|p_2|}{2}<\dfrac{|p_1|+|p_1|}{2}=|p_1|,$$从而有$M(a,b)\in X$．
(3) 如图，$D$表示直线$y=x-1$与抛物线$y=\dfrac 14(x+1)^2-\dfrac 54$所围成的封闭区域(包含边界)，其中$A(0,-1)$，$B(2,1)$是直线与抛物线的两个交点．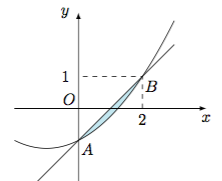
当点$(p,q)\in D$时，有$$\dfrac 14(p+1)^2-\dfrac 54\leqslant q\leqslant p-1,$$从而$$(p-2)^2\leqslant p^2-4q\leqslant 4-2p,$$其中$0\leqslant p\leqslant 2$．于是有$$\dfrac{p+|p-2|}{2}\leqslant \varphi(p,q) =\dfrac{p+\sqrt{p^2-4q}}{2}\leqslant \dfrac{p+\sqrt{4-2p}}{2},$$从而$$\varphi(p,q)\geqslant \dfrac{p+2-p}2=1,$$因此$\varphi_{\min}=1$．
设$\sqrt{4-2p}=t$，其中$t\in[0,2]$，则$$\dfrac{p+\sqrt{4-2p}}{2}=\dfrac{\dfrac{4-t^2}2+t}2=-\dfrac{-(t-1)^2+5}{4}\leqslant \dfrac 54,$$所以$\varphi_{\max}=\dfrac 54$．
综上所述，$\varphi_{\min}=1$且$\varphi_{\max}=\dfrac 54$．