如图，已知椭圆$\dfrac{x^2}4+y^2=1$的上顶点为$A$，过点$A$作圆$M:(x+1)^2+y^2=r^2$($0<r<1$)的两条切线分别与椭圆$C$相交于点$B,D$(不同于点$A$)．当$r$变化时，试问直线$BD$是否过某个定点？若是，求出该定点；若不是，请说明理由．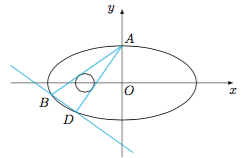
分析与解 设$AB:y=kx+1$，则有$$\dfrac{|k-1|}{\sqrt{1+k^2}}=r,$$于是$$\left(1-r^2\right)k^2-2k+1-r^2=0,$$于是可得直线$AD$的斜率为$\dfrac 1k$．联立直线$AB$与椭圆的方程，可得$$\left(4k^2+1\right)x^2+8kx=0,$$于是可得$$B\left(\dfrac{-8k}{4k^2+1},\dfrac{-4k^2+1}{4k^2+1}\right),D\left(\dfrac{-8k}{4+k^2},\dfrac{-4+k^2}{4+k^2}\right).$$考虑到当$r\to 1$时，$D$趋于椭圆的下顶点，$B$趋于椭圆的上顶点，因此猜想定点若存在，则必然在$y$轴上，因此计算直线$BD$的纵截距，为$$\dfrac{\dfrac{-4k^2+1}{4k^2+1}\cdot \left(\dfrac{-8k}{4+k^2}\right)+\dfrac{8k}{4k^2+1}\cdot \dfrac{-4+k^2}{4+k^2}}{\dfrac{-8k}{4+k^2}+\dfrac{8k}{4k^2+1}}=-\dfrac 53,$$因此直线$BD$过定点$\left(0,-\dfrac 53\right)$．
思考与总结 找到直线$AB$和直线$AD$之间的相关关系是解决问题的关键．
最后一步求BD的纵截距怎么来的？