如图，正方体$ABCD-A_1B_1C_1D_1$的棱长为$2$，动点$E,F$在棱$A_1B_1$上，动点$P,Q$分别在棱$AD,CD$上，若$EF=1$，$A_1E=x$，$DQ=y$，$DP=z$，且$x,y,z>0$，则四面体$PEFQ$的体积（ ）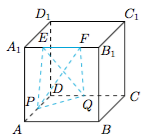
A．与$x,y,z$都有关
B．与$x$有关，与$y,z$无关
C．与$y$有关，与$x,z$无关
D．与$z$有关，与$x,y$无关
分析与解 延长$QP$与$BA$交于点$R$，如图．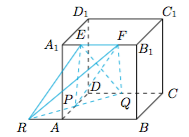
根据题意，四面体$PEFQ$的体积$$V_{P-EFQ}=\dfrac{PQ}{RQ}\cdot V_{R-EFQ}=\dfrac{PQ}{RQ}\cdot V_{Q-EFR}=\dfrac{PD}{AD}\cdot V_{Q-EFR},$$而$\triangle REF$的面积及$Q$到平面$EFR$的距离均为定值，因此四面体$PEFQ$的体积只与$P$点的位置有关，选项D正确．
注 本题对体积的转化是一种常用的方式．当然也可以通过转化底面解决这个问题：选定$\triangle EFQ$为底面，则点$P$到平面$EFQ$的距离为高．因为$\triangle EFQ$的面积不变，与$x,y$无关，而高与$z$相关，故D正确．