若存在$a\in\mathcal R$，使关于$x$的不等式$x|x-a|<m$在$[0,1]$上恒成立，则实数$m$的取值范围是_______．
分析与解 问题的关键在于求出当$a\in\mathcal R$，$x\in[0,1]$时，函数$f(x)=x|x-a|$的最大值$M(a)$的最小值．易知$$M(a)=\begin{cases} \max\left\{f\left(\dfrac{a}2\right),f(1)\right\},&a\in [0,2],\\ f(1),&a\in (-\infty,0)\cup (2,+\infty).\end{cases} $$如图，当$0<a<2$且$f\left(\dfrac a2\right)=f(1)$时，函数$M(a)$取得最小值．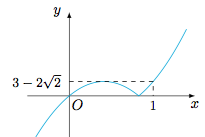
此时$\dfrac{a^2}4=1-a$，解得$a=-2+2\sqrt 2$，于是$M(a)$的最小值为$3-2\sqrt 2$，进而实数$m$的取值范围是$(3-2\sqrt 2,+\infty)$．
注 本题关键在于仔细读题，理解实数$m$的真实含义．