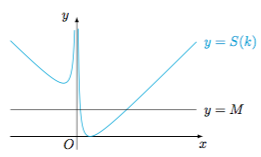
在平面直角坐标系中，过点 $P\left(a,b\right)\left(a\ne 0,b\ne 0\right)$ 的直线 $l$ 与两坐标轴围成的三角形的面积是定值 $M$，则这样的直线可能有_____条．
分析与解 设直线$l$的斜率为$k$，$k\neq 0$且$k\neq \dfrac ba$，直线$l$与两坐标轴围成的三角形的面积为$S(k)$．
定性分析 不妨设$a,b>0$．如左图所示，当$k\in (-\infty,0)$时，$S(k)$先从正无穷大单调递减，当$P$为直线$l$被两坐标轴所截得的线段的中点时取得最小值，再单调递增到正无穷大；当$k\in \left(0,\dfrac ba\right)$时，$S(k)$从正无穷大单调递减到$0$；当$k\in\left(\dfrac ba,+\infty\right)$时，$S(k)$从$0$单调递增到正无穷大．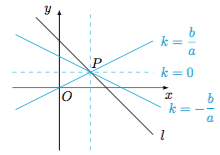
因此不同的$M$($M>0$)对应的$k$的值可能为$2,3,4$个，进而这样的直线可能有$2,3,4$条．
定量计算 直线$l:y=k(x-a)+b$，于是直线$l$与两坐标轴围成的三角形的面积$$\begin{split}S(k)=&\dfrac 12\left|-\dfrac{b}{k}+a\right|\cdot\left|-ak+b\right|\\=&\dfrac 12\left|a^2k+\dfrac{b^2}{k}-2ab\right|\\=&\dfrac 12\left[a^2|k|+\dfrac{b^2}{|k|}-2ab\cdot \dfrac{k}{|k|}\right],\end{split}$$因此$S(k)$的函数图象如图：
不同的$M$($M>0$)对应的$k$的值可能为$2,3,4$个，因此这样的直线可能有$2,3,4$条．