已知函数$f(x)=\dfrac{(x-1)\ln x}{x}$，且$f(x_1)=f(x_2)$，$x_1\neq x_2$，求证：$x_1+x_2>2$．
分析与解 对$f(x)$求导得$$f'(x)=\dfrac {x-1+\ln x}{x^{2}}.$$当$x=1$时，$f(x)$取到极小值$0$，构造二次函数$g(x)=(x-1)^2$，考虑函数$$f(x)-g(x)=\dfrac {x-1}{x}(\ln x-x^{2}+x),$$记$h(x)=\ln x-x^2+x$，则$$h'(x)=\dfrac 1x-2x+1=\dfrac {(1-x)(1+2x)}{x}.$$所以$h(x)$在$(0,1)$上单调递增，在$(1,+\infty)$上单调递减．又因为$h(1)=0$，所以$h(x)\leqslant 0$．
从而有当$x\in(0,1)$时，$f(x)>g(x)$；当$x\in(1,+\infty)$时，$f(x)<g(x)$．
因为$f(x_1)=f(x_2)>0$，所以存在$x_3<1<x_4$，满足$$g(x_3)=g(x_4)=f(x_1)=f(x_2),$$结合上面$f(x)$与$g(x)$有大小关系有$x_3<x_1<1<x_4<x_2$，从而有$x_1+x_2>x_3+x_4=2$．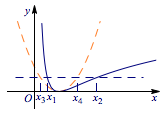
注 通过构造二次函数去证明极值点的偏移，常用于解决偏移的中心对应的是极值点的情况，可以有效地减少运算量．所构造的二次函数的极值点与题中函数的极值点重合，且极值相等，通过二次函数的对称性，以及它与函数在极值点两侧的位置关系就可以得到想要的结果．