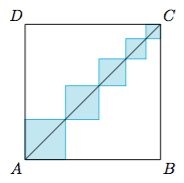
如图，在正方形 $ABCD$ 内，有五个边长是不同的整数的正方形，且它们的一条对角线都在 $AC$ 上，且 $AB$ 长是 $2015$，求这五个正方形的面积之和的最大值及最小值．
分析与解 改造的切割线方法来自学大的王举老师，代数变形的方法来自山西的李有贵老师．
切割线放缩 设这五个正方形的边长分别为$x_i$($i=1,2,3,4,5$)，考虑函数$f(x)=x^2$的割线，记$l(m,n)$($m\leqslant n$)为过函数$y=f(x)$图象上的点$M(m,m^2)$和$N(n,n^2)$的割线(当$m=n$时，将函数$f(x)$在$x=m$处的切线视为$l(m,n)$)．显然当$x<m$或$x>n$时，$f(x)$的图象在$l(m,n)$上方；当$m<x<n$时，$f(x)$的图象在$l(m,n)$下方，如图．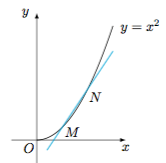
由于$x_1,x_2,x_3,x_4,x_5$中至少有两个数在集合$$\{x\in\mathcal N^*\mid x\leqslant 401\lor x\geqslant 405\}$$中，不妨设为$x_1,x_2$；又$x_1,x_2,x_3,x_4,x_5$中至少有四个数在集合$$\{x\in\mathcal N^*\mid x\leqslant 402\lor x\geqslant 404\}$$中，设其中不同于$x_1,x_2$的数为$x_3,x_4$；剩下的一个数为$x_5$，注意到$$l(401,405),l(402,404),l(403,403)$$的斜率均相等，记为$k$，则有$$\begin{cases} x_1^2\geqslant k(x_1-401)+401^2,\\ x_2^2\geqslant k(x_2-405)+405^2,\\ x_3^2\geqslant k(x_3-402)+402^2, \\ x_4^2\geqslant k(x_4-404)+404^2, \\ x_5^2\geqslant k(x_5-403)+403^2,\end{cases} $$累加有$$x_1^2+x_2^2+x_3^2+x_4^2+x_5^2\geqslant 401^2+402^2+403^2+404^2+405^2,$$等号当$$x_1=401,x_2=405,x_3=402,x_4=404,x_5=403$$时取得，因此所求的最小值为$812055$．
接下来考虑最大值，由于$x_1,x_2,x_3,x_4,x_5$中至少有两个数在集合$\{x\in\mathcal N^*\mid 4\leqslant x\leqslant 2005\}$中，不妨设为$x_1,x_2$；又$x_1,x_2,x_3,x_4,x_5$中至少有三个数在集合$$\{x\in\mathcal N^*\mid 3\leqslant x\leqslant 2006\}$$中，设其中不同于$x_1,x_2$的数为$x_3$；又$x_1,x_2,x_3,x_4,x_5$中至少有四个数在集合$$\{x\in\mathcal N^*\mid 2\leqslant x\leqslant 2007\}$$中，设其中不同于$x_1,x_2,x_3$的数为$x_4$；剩下的一个数为$x_5$，注意到$$l(4,2005),l(3,2006),l(2,2007),l(1,2008)$$的斜率均相等，记为$k'$，则有$$\begin{cases} x_1^2\leqslant k'(x_1-4)+4^2,\\ x_2^2\leqslant k'(x_2-2005)+2005^2,\\ x_3^2\leqslant k'(x_3-3)+3^2, \\ x_4^2\leqslant k'(x_4-2)+2^2, \\ x_5^2\leqslant k'(x_5-1)+1^2,\end{cases} $$累加有$$x_1^2+x_2^2+x_3^2+x_4^2+x_5^2\leqslant 1^2+2^2+3^2+4^2+2005^2,$$等号当$$x_1=4,x_2=2005,x_3=3,x_4=2,x_5=1$$时取得，因此所求的最大值为$4020055$．
思考与总结 这种方法是切割线放缩的改造，经过改造后可以适应于变量为整数的情形．
代数变形 设这五个正方形的边长分别为$$x_1+1,x_2+2,x_3+3,x_4+4,x_5+5,x_i\in\mathcal N,$$且$x_1\leqslant x_2\leqslant x_3\leqslant x_4\leqslant x_5$，于是$$x_1+x_2+x_3+x_4+x_5=2000.$$由于$$5\sum_{i=1}^na_i^2=(a_1+a_2+a_3+a_4+a_5)^2+\sum_{1\leqslant i<j\leqslant 5}(a_j-a_i)^2,$$于是\[\begin{split} 5\sum_{i=1}^5{(x_i+i)^2}=2015^2&+(x_2-x_1+1)^2+(x_3-x_1+2)^2+(x_4-x_1+3)^2+(x_5-x_1+4)^2\\ &+(x_3-x_2+1)^2+(x_4-x_2+2)^2+(x_5-x_2+3)^2\\ &+(x_4-x_3+1)^2+(x_5-x_3+2)^2+(x_5-x_4+1)^2,\end{split} \]显然当$x_1=x_2=x_3=x_4=x_5=400$时取得最小值$$401^2+402^2+403^2+404^2+405^2=812055.$$
另一方面，由于$400\leqslant x_5\leqslant 2000$，有\[\begin{split} \sum_{i=1}^5{(x_i+i)^2}&=2015^2-2\big[(x_5+5)(x_1+x_2+x_3+x_4+10)+(x_4+4)(x_1+x_2+x_3+6)\\ &\qquad\qquad\qquad \qquad\qquad+(x_3+3)(x_1+x_2+3)+(x_2+2)(x_1+1)\big]\\ &=2015^2-2\big[(x_5+5)(2010-x_5)+(x_4+4)(x_1+x_2+x_3+6)\\&\qquad\qquad\qquad \qquad\qquad+(x_3+3)(x_1+x_2+3)+(x_2+2)(x_1+1)\big]\\ &\leqslant 2015^2-2\big[(2000+5)(2010-2000)+4\cdot 6+3\cdot 3+2\cdot 1\big],\end{split} \]等号当且仅当$x_1=x_2=x_3=x_4=0$，$x_5=2000$时取得，因此所求的最大值为$$1^2+2^2+3^2+4^2+2005^2=4020055.$$
思考与总结 利用对$\displaystyle \sum\limits_{i=1}^n{x_i^2}$的两种常用代数变形求最值．