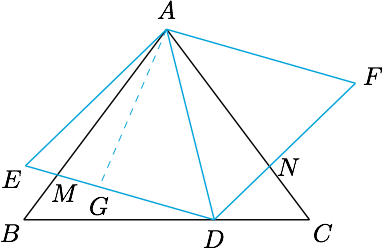
已知等腰三角形$ABC$的底$BC$长为$6$，腰$AB$长为$5$．设$D$是底边$BC$上一点，以$AD$为边向两边作等边三角形$ADE,ADF$，设$DE,DF$分别交$AB,AC$于点$M,N$，求证：当$D$位于$BC$中点时$DM+DN$取得最小值．
分析与解 考虑到问题的对称性，我们采用对称的方式设参数：设$\angle MDB=\dfrac {\pi}6-x$，$\angle NDC=\dfrac{\pi}6+x$，其中$x\in [-\theta,\theta]$，$\theta$是临界状态时的角．
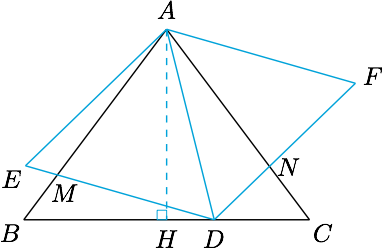作$AH\perp BC$于$H$，则$\angle DAH=x$，于是$$BD=3+4\tan x,CD=3-4\tan x,$$而$$\dfrac{DM}{\sin B}=\dfrac{BD}{\sin\left(B+\dfrac{\pi}6-x\right)},\dfrac{DN}{\sin C}=\dfrac{CD}{\sin\left(C+\dfrac{\pi}6+x\right)},$$于是\[\begin{split} \dfrac{DM+DN}{\sin B}&=\dfrac{3+4\tan x}{m\cos x-n\sin x}+\dfrac{3-4\tan x}{m\cos x+n\sin x}\\ &=\dfrac{6m\cos^2x+8n\sin^2x}{\cos x(m^2\cos^2x-n^2\sin^2x)},\end{split} \]其中$m=\sin\left(B+\dfrac{\pi}6\right)$，$n=\cos\left(B+\dfrac{\pi}6\right)$．因此当$x=0$时，$DM+DN$取得最小值，此时$D$位于$BC$的中点．
几何证明
在$DE$上取$DG=FN$，则$\triangle ADN$与$\triangle AEG$全等，因此$$DM+DN=DM+GE=DE+GM=AD+GM,$$而当$D$位于$BC$中点时，$AD$和$GM$同时取得最小值（注意$G$点的轨迹是延长线通过点$A$的线段）．（说明：$\angle CAG=\dfrac {\pi}{3}$，所以$\angle BAG$为定值．当$AD$减小时，$\angle AGD$增大，在$\triangle GAD$中得到$AG$减小；在$\triangle MAG$中，$\angle GMA$增大，所以$MG$减小．）
最后给出一个练习题．
如图，沿$DE$折叠一张边长为$2$等边三角形的纸片$ABC$，使顶点$A$落在边$BC$的点$A'$上．选择合适的变量研究折痕$DE$的长度$l$的变化，求出$l$的最大值与最小值，并给出相应的几何证明．
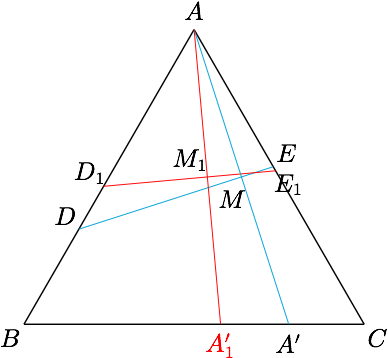
答案 如图，连接$AA'$，设其中点为$M$．
设$\angle CAA'=30^\circ -x$，$\angle BAA'=30^\circ +x$，其中$-30^\circ\leqslant x\leqslant 30^\circ$．
在三角形$ACA'$中应用正弦定理，有$$\dfrac{AA'}{\sin C}=\dfrac{AC}{\sin (C+\angle CAA')},$$于是$$AA'=\dfrac{\sqrt 3}{\cos x},$$进而\[\begin{split} DE&=DM+ME\\& =AM\cdot\left(\tan\angle DAA'+\tan\angle CAA'\right)\\ &=AM\cdot\left[\tan(30^\circ+x)+\tan(30^\circ-x)\right]\\ &=AM\cdot \left(\dfrac{\dfrac{\sqrt 3}3+\tan x}{1-\dfrac{\sqrt 3}3\tan x}+\dfrac{\dfrac{\sqrt 3}3-\tan x}{1+\dfrac{\sqrt 3}3\tan x}\right)\\ &=\dfrac{2\sqrt 3\cdot AM}{4\cos^2x-1}\\ &=\dfrac {3}{\cos x\cdot (4\cos^2x-1)},\end{split} \]因此当$x\in\left[-\dfrac{\pi}6,0\right]$时，$DE$的长对应的函数$l(x)$单调递减；当$x\in\left[0,\dfrac{\pi}6\right]$时，函数$l(x)$单调递增．当$x=\pm\dfrac{\pi}6$时，$l(x)$取得最大值，为$\sqrt 3$；当$x=0$时，$l(x)$取得最小值，为$1$．
几何证明
只考虑$A'$在$BC$的中点右侧（含中点）的情形即可，当$A_1'C>A'C$时，如图，由于$AA'_1<AA'$，于是$AM_1<AM$，因此过$M$作$D_1E_1$的平行线，分别交$AB,AC$于$D',E'$，则$D_1E_1<D'E'$（图中未画出）．
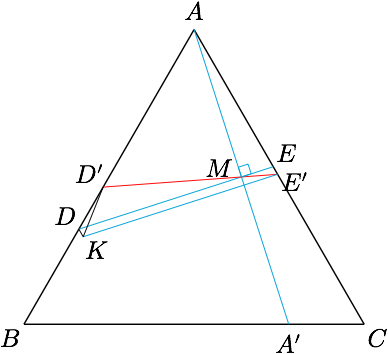
接下来证明$D'E'<DE$．如图，作$DK$与$EE'$平行且相等，连接$DK,D'K$．
显然$MD>ME$，于是$$\dfrac{DD'}{\sin\angle DMD'}=\dfrac{MD}{\sin \angle DD'M}>\dfrac{ME}{\sin\angle ME'E}=\dfrac{EE'}{\sin\angle EME'},$$因此$DD'>EE'$，从而$DD'>DK$，于是$\angle DKD'>\angle DD'K$．因此$$\angle KD'E'=180^\circ-\angle AD'E'-\angle DD'K>120^\circ-\angle DKD'>\angle D'KE',$$于是在$\triangle D'KE'$中，有$KE'>D'E'$，即$DE>D'E'$，因此命题得证．
其他方法（由诗冭提供）
记$\triangle ADE$与$\triangle A'DE$的外心分别为$O,O'$，则$OO'\perp DE$，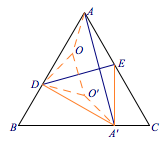
从而有$$\angle DOO'=\dfrac 12\angle DOE=\dfrac {\pi}{3},$$所以$\triangle ODD'$为正三角形，有$$DE=2OD\cos\dfrac{\pi}{6}=\sqrt 3OD.$$且$$OO'=OA=O'A'.$$又因为$$\angle DOA=2\angle DEA=\angle A'EA,$$所以$\angle DAO=\angle A'AE$，记此角为$\theta$，则$$\angle OAA'=\dfrac {\pi}{3}-2\theta.$$又因为$OO'\parallel AA'$，所以$$AA'=2OA\cdot\cos\left(\dfrac {\pi}{3}-2\theta\right )+OO'=OA\cdot\left(1+2\cos\left(\dfrac {\pi}{3}-2\theta\right )\right ).$$于是有$$DE=\dfrac {\sqrt 3AA'}{1+2\cos\left(\frac{\pi}{3}-2\theta\right )}.$$当$A'$为$BC$中点时，$AA'$有最小值$\sqrt 3$，同时$\theta$有最大值$\dfrac {\pi}{6}$，对应$DE$的最小值$1$；当$A'$与$C$重合时，$AA'$有最大值$2$，$\theta$有最小值$0$，对应$DE$的最大值$\sqrt 3$．