每日一题[488]两边夹

若不等式$\left(\dfrac{1}{x-1}+a\right)\cdot \ln x > 1$对一切$x>0$且$x\neq 1$均成立，求实数$a$的值．

---

分析    首先分析端点，当$x\to 0$和$x \to +\infty$时，可得$0\leqslant a\leqslant 1$．于是可得

$$\dfrac{1}{x-1}+a=\dfrac{ax-a+1}{x-1}$$ 的分子部分恒正，接下来利用它“清君侧”即可．

解    易知$0\leqslant a\leqslant 1$，于是原不等式等价于

$$\varphi(x)=\ln x-\dfrac{x-1}{ax-a+1}\begin{cases} <0,0<x<1,\\ >0,x>1.\end{cases}$$ 注意到$\varphi (1)=0$，而其导函数 $$\varphi'(x)=\dfrac{[a^2x-(1-a)^2]\cdot (x-1)}{x(ax-a+1)^2},$$ 接下来根据$a$与$\dfrac 12$的大小关系展开讨论．

第一种情形，$a=\dfrac 12$．此时在$(0,+\infty)$上，$\varphi'(x)\geqslant 0$，于是$\varphi(x)$在$(0,+\infty)$上单调递增，结合$\varphi(1)=0$，符合题意；

第二种情形，$a=0$．此时在$(1,+\infty)$上，$\varphi'(x)<0$，于是在$(1,+\infty)$上，$\varphi(x)<\varphi(1)=0$，不符合题意；

第三种情形，$0<a<\dfrac 12$．此时在$\left(1,\left(\dfrac 1a-1\right )^2\right)$上，$\varphi'(x)<0$，于是在$\left(1,\left(\dfrac 1a-1\right )^2\right)$上，$\varphi(x)<\varphi(1)=0$，不符合题意；

第四种情形，$\dfrac 12<a\leqslant 1$．此时在$\left(\left(\dfrac 1a-1\right )^2,1\right)$上，$\varphi'(x)<0$，于是在$\left(\left(\dfrac 1a-1\right )^2,1\right)$上，$\varphi(x)>\varphi(1)=0$，不符合题意．

综上，实数$a$的值为$\dfrac 12$．

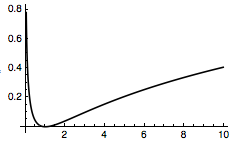
此时函数$y=\left(\dfrac 1{x-1}+\dfrac 12\right )\cdot \ln x-1$的图象如图：

下面附上一道练习题．

已知$f(x)=\dfrac{\ln (x+1)}{{\rm e}^x-1}+ax$．若对任意$x>-1$且$x\neq 0$，均有$f(x)>1$恒成立，求实数$a$的值．

答案    $1$．