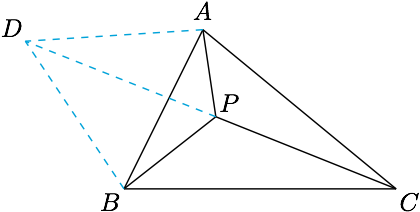
已知锐角三角形$ABC$中一点$P$满足$\angle APB=\angle BPC=\angle CPA=120^\circ$,求证:$$S_{\triangle BPC}:S_{\triangle CPA}:S_{\triangle APB}=\dfrac{\sin A}{\sin (A+60^\circ)}:\dfrac{\sin B}{\sin (B+60^\circ)}:\dfrac{\sin C}{\sin (C+60^\circ)}.$$
证明 如图作等边三角形$ABD$,连接$PD$,由费马点的性质易知$C,P,D$三点共线.
于是有$$\dfrac{S_{\triangle BPC}}{S_{\triangle CPA}}=\dfrac{\dfrac 12\cdot PC\cdot BC\cdot \sin\angle PCB}{\dfrac 12\cdot PC\cdot AC\cdot \sin\angle PCA}=\dfrac{BC}{AC}\cdot \dfrac{\sin\angle PCB}{\sin\angle PCA}.$$在$\triangle ABC$中应用正弦定理,有$$\dfrac{BC}{AC}=\dfrac{\sin A}{\sin B};$$在$\triangle CAD$和$\triangle CBD$中应用正弦定理有$$\dfrac{CD}{\sin (A+60^\circ)}=\dfrac{AD}{\sin\angle ACP},\dfrac{CD}{\sin (B+60^\circ)}=\dfrac{BD}{\sin\angle BCP},$$因此$$\dfrac{\sin\angle PCB}{\sin\angle PCA}=\dfrac{\sin (B+60^\circ)}{\sin (A+60^\circ)};$$综上,有$$S_{\triangle BPC}:S_{\triangle CPA}=\dfrac{\sin A}{\sin (A+60^\circ)}:\dfrac{\sin B}{\sin (B+60^\circ)},$$因此原命题得证.