每日一题[65] 利用极端原理构造

已知集合\(S=\left\{a_1,a_2,a_3,\cdots,a_n\right\}\)（\(n\geqslant 3\)），集合\(T\subseteq\left\{\left(x,y\right)\left|x\in S,y\in S,x\neq y\right.\right\}\)且满足\(\forall a_i,a_j\in S\)（\(i,j=1,2,3,\cdots,n,i\neq j\)），\(\left(a_i,a_j\right)\in T\)与\(\left(a_j,a_i\right)\in T\)恰有一个成立．对于\(T\)定义\[d_T(a,b)=\begin{cases}1,(a,b)\in T,\\0,(b,a)\in T,\end{cases}\]以及\[l_T\left(a_i\right)=d_T\left(a_i,a_1\right)+d_T\left(a_i,a_2\right)+\cdots+d_T\left(a_i,a_{i-1}\right)+d_T\left(a_i,a_{i+1}\right)+\cdots+d_T\left(a_i,a_n\right),i=1,2,3,\cdots,n.\]

（1）若\(n=4\)，\(\left(a_1,a_2\right)\)，\(\left(a_3,a_2\right)\)，\(\left(a_2,a_4\right)\in T\)，求\(l_T\left(a_2\right)\)的值及\(l_T\left(a_4\right)\)的最大值；

（2）从\(l_T\left(a_1\right)\)，\(l_T\left(a_2\right)\)，\(\cdots\)，\(l_T\left(a_n\right)\)中任意删去两个数，记剩下的\(n-2\)个数的和为\(M\)．求证：\[M\geqslant \dfrac 12n(n-5)+3.\]

（3）对于满足\(l_T\left(a_i\right)<n-1\)（\(i=1,2,3,\cdots,n\)）的每一个集合\(T\)，集合\(S\)中是否都存在三个不同的元素\(e\)，\(f\)，\(g\)，使得\[d_T\left(e,f\right)+d_T\left(f,g\right)+d_T\left(g,e\right)=3\]恒成立，并说明理由．

（1）我们引入“坐标”来理解题意．将\(\left(a_i,a_j\right)\in T\)用坐标\(\left(i,j\right)\)的位置打“√”表示，相应地，此时\(\left(a_j,a_i\right)\not\in T\)用坐标\(\left(j,i\right)\)的位置打“×”表示．这样一来就有任何一个“√”关于\(y=x\)对称的位置均为“×”，且\(l_T\left(a_i\right)\)表示第\(i\)列中的“√”的总数．那么有下图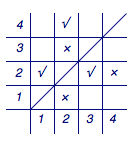． 从而\(l_T\left(a_2\right)=1\)，且\(l_T\left(a_4\right)\)最大为\(2\)； （2）根据题意得\[\begin{split}M&\geqslant \sum_{i=1}^n{l_T\left(a_i\right)}-\left(n-1\right)-\left(n-2\right)\\&=\dfrac{1}{2}n\left(n-1\right)-2n+3\\&=\dfrac 12n^2-\dfrac 52n+3,\end{split}\]于是原不等式成立． （3）答案是肯定的，这里需要利用极端原理进行构造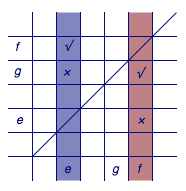． 如图，设\(l_T{\left(a_f\right)}\)最大．根据题意\(l_T{\left(a_f\right)}\leqslant{n-1}\)，于是第\(f\)列中必然存在一个“×”，设其坐标为\(\left(f,e\right)\)，于是在\(\left(e,f\right)\)处为“√”． 逐行比较第\(e\)列和第\(f\)列中的数．由于这两列在第\(f\)行和第\(e\)行的较量中第\(e\)列多出一个“√”，因此在其他行的较量中必然存在某一行为第\(e\)列为“×”而第\(f\)列为“√”的情况（否则与\(l_T{\left(a_f\right)}\)最大矛盾），设该行为第\(g\)行． 这样一来，我们就有坐标\(\left(e,f\right)\)，\(\left(f,g\right)\)，\(\left(g,e\right)\)处均为“√”，命题得证．