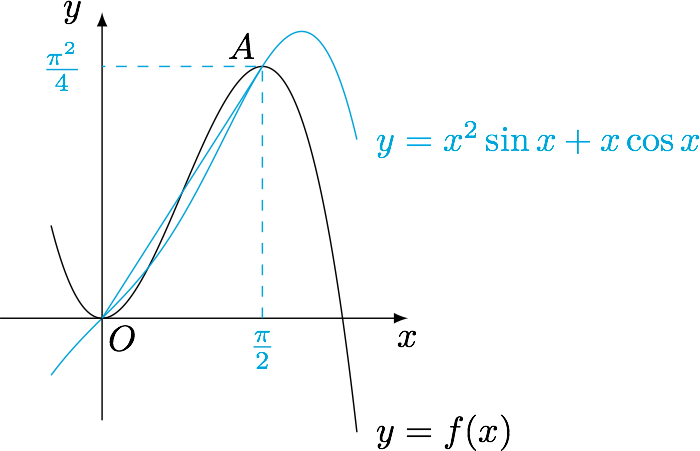已知函数$f(x)=ax^3+bx^2+cx+d$在$O,A$两点处取得极值,其中$O$是坐标原点,$A$在曲线$y=x^2\sin x+x\cos x$($x\in\left[\dfrac{\pi}3,\dfrac{2{\pi}}3\right]$)上,则曲线$y=f(x)$的切线的斜率的最大值是_______.
解 根据已知,$f(x)$的导函数$f'(x)=3ax^2+2bx+c$.由于函数$f(x)$在$O$处取得极值,于是$$f(0)=f'(0)=0,$$即$c=d=0$,因此$$f(x)=ax^3+bx^2.$$且由于$A$必然位于第一象限,因此$a<0$.曲线$y=f(x)$的切线的斜率的最大值,即$f'(x)$的最大值,为$$\max (k)=-\dfrac{b^2}{3a},$$因此接下来的任务是建立$\max (k)$与$A$点的联系.不难求得$A$点的坐标为$\left(-\dfrac {2b}{3a},\dfrac{4b^3}{27a^2}\right)$,因此直线$OA$的斜率$$k_{OA}=-\dfrac{2b^2}{9a}=\dfrac 23\max (k),$$于是求只要求出$k_{OA}$的最大值即可.
由于$A$在曲线$y=x^2\sin x+x\cos x$($x\in\left[\dfrac{\pi}3,\dfrac{2{\pi}}3\right]$)上,设$A$的横坐标为$x$,则$$k_{OA}=g(x)=x\sin x+\cos x,$$其导函数$$g'(x)=x\cos x,$$于是当$x=\dfrac{\pi}2$时,$k_{OA}$取得最大值为$g\left(\dfrac{\pi}2\right)=\dfrac{\pi}2$,进而可知所求的最大值为$\dfrac{3\pi}4$.