已知$\triangle ABC$中,$A=120^\circ$,$D$为$BC$边上的中点,$E,F$分别为$AB,AC$边上的动点,且$EF\parallel BC$,求证:$DE+DF\geqslant BD$. 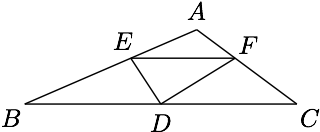
证明 设$\overrightarrow{AE}=\lambda \overrightarrow{AB}$,$\overrightarrow{AF}=\lambda \overrightarrow{AC}$,记$AB=c$,$AC=b$,则$$\overrightarrow{AB}\cdot \overrightarrow{AC}=-\dfrac 12bc,BD=\dfrac 12\sqrt{b^2+c^2+bc}.$$
由$\overrightarrow{AD}=\dfrac 12\overrightarrow{AB}+\dfrac 12\overrightarrow{AC}$,可得$$\overrightarrow{DE}=\left(\lambda -\dfrac 12\right)\overrightarrow{AB}-\dfrac 12\overrightarrow{AC},$$且$$\overrightarrow{DF}=-\dfrac 12\overrightarrow{AB}+\left(\lambda-\dfrac 12\right)\overrightarrow{AC},$$从而$$DE+DF=\sqrt{\left(\lambda-\dfrac 12\right)^2c^2+\dfrac 14b^2+\dfrac 12\left(\lambda-\dfrac 12\right)bc}+\sqrt{\left(\lambda-\dfrac 12\right)^2b^2+\dfrac 14c^2+\dfrac 12\left(\lambda-\dfrac 12\right)bc},$$欲证不等式即$$\sqrt{x^2c^2+b^2+xbc}+\sqrt{x^2b^2+c^2+xbc}\geqslant \sqrt{b^2+c^2+bc},$$其中$x=2\lambda -1$,也即$$b^2+c^2+x^2(b^2+c^2)+2xbc+2\sqrt{(x^2c^2+b^2+xbc)\cdot(x^2b^2+c^2+xbc)}\geqslant b^2+c^2+bc.$$考虑到$$x^2c^2+b^2+xbc=\left(xc+\dfrac 12b\right)^2+\dfrac 34b^2\geqslant\dfrac 34b^2,$$类似的,有$$x^2b^2+c^2+xbc\geqslant \dfrac 34c^2,$$于是\[\begin{split} LHS&\geqslant b^2+c^2 +\left(2x^2+2x+\dfrac 32\right)bc\\ &=b^2+c^2+\left[1+\dfrac 12(2x+1)^2\right]bc \\ &\geqslant b^2+c^2+bc,\end{split} \]等号当且仅当$b=c$,$\lambda=\dfrac 14$时取得,因此原命题得证.

