每日一题[64] 萌萌的参数方程

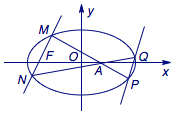
已知\(MN\)是过椭圆\(\dfrac{x^2}9+\dfrac{y^2}5=1\)的左焦点\(F\)的直线（\(M,N\)在椭圆上），\(A(1,0)\)是椭圆长轴上的一个定点．直线\(MA\)，\(NA\)分别交椭圆于\(P\)、\(Q\)，求证：直线\(PQ\)与直线\(MN\)的斜率之比为定值．

 法一

设\(M\left(x_1,y_1\right)\)，\(N\left(x_2,y_2\right)\)，\(P\left(x_3,y_3\right)\)，\(Q\left(x_4,y_4\right)\)．

由\(M\)、\(F\)、\(N\)三点共线，有\[\dfrac{y_1}{x_1+2}=\dfrac{y_2}{x_2+2},\]化简得\[x_1y_2-x_2y_1=2\left(y_2-y_1\right).\qquad\cdots (*)\]

直线\(MA\)的方程为\[MA:x=\dfrac{x_1-1}{y_1}y+1,\]代入椭圆方程中得\[\dfrac{5\left(x_1-1\right)^2+9y_1^2}{y_1^2}\cdot y^2+\dfrac{10\left(x_1-1\right)}{y_1}\cdot y-40=0,\]将\(9y_1^2=45-5x_1^2\)代入，有\[\dfrac{5-x_1}{y_1^2}\cdot y^2+\dfrac{x_1-1}{y_1}\cdot y-4=0,\]从而\[y_1\cdot y_3=\dfrac{4y_1}{x_1-5},\]于是\[y_3=\dfrac{4y_1}{x_1-5}.\]

将\(y_3\)代入直线\(MA\)的方程，有\[x_3=\dfrac{5x_1-9}{x_1-5}.\]

同理可得\[x_4=\dfrac{5x_2-9}{x_2-5},y_4=\dfrac{4y_2}{x_2-5}.\]

因此直线\(PQ\)的斜率为\[\dfrac{\dfrac{4y_1}{x_1-5}-\dfrac{4y_2}{x_2-5}}{\dfrac{5x_1-9}{x_1-5}-\dfrac{5x_2-9}{x_2-5}}=\dfrac{-20\left(y_1-y_2\right)-4\left(x_1y_2-x_2y_1\right)}{-16\left(x_1-x_2\right)},\]将(*)代入，即得直线\(PQ\)与直线\(MN\)的斜率之比为\(\dfrac 74\)，是定值．

 法二

首先对椭圆的参数方程，有以下常用引理．

设点\(A\left(a\cos{2\alpha},b\sin{2\alpha}\right)\)，\(B\left(b\cos{2\beta},b\sin{2\beta}\right)\)，则直线\(AB\)的方程为\[AB:y=-\dfrac{b}{a}\cdot \dfrac{1}{\tan\left(\alpha+\beta\right)}x+b\cdot\dfrac{1+\tan\alpha\cdot\tan\beta}{\tan\alpha+\tan\beta},\]特别的，若直线\(AB\)过点\((m,0)\)，那么有\[\tan\alpha\cdot\tan\beta=\dfrac{m-a}{m+a}.\]

由此引理，很容易证明并推广本题结论．

最后给出一道练习题．

在平面直角坐标系\(xOy\)中，椭圆\(\dfrac{x^2}{2}+y^2=1\)的左、右焦点分别为\(F_1\)、\(F_2\)，\(A\)是椭圆上位于第一象限内的一点，直线\(AF_1\)、\(AF_2\)分别与椭圆交于点\(C\)、\(B\)，直线\(BF_1\)与椭圆交于点\(P\)，连接\(CD\)，直线\(AD\)与\(BC\)交于点\(E\)．设直线\(AF_2\)的斜率为\(k\)，直线\(CD\)的斜率为\(k'\)．

（1）证明：\(\overrightarrow{AF_1}\cdot \overrightarrow{AF_2}<2\)；

（2）证明：\(\dfrac{k'}{k}\)为常数；

（3）证明：点\(E\)在定直线上．