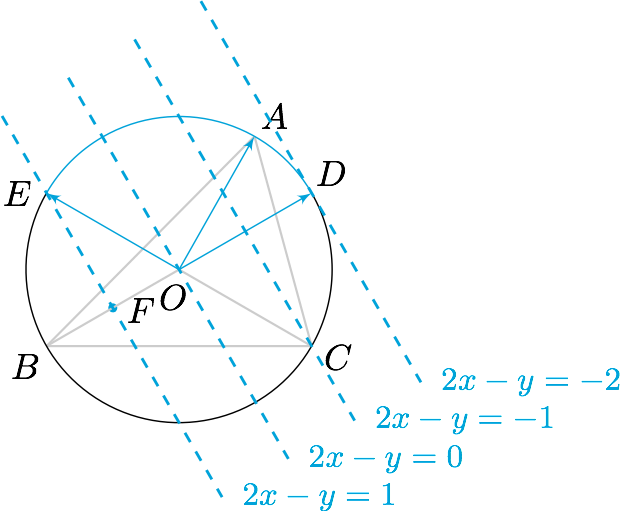已知$O$为锐角三角形$ABC$的外心,$A=\dfrac{\pi}3$,且$\overrightarrow{OA}=x\overrightarrow{OB}+y\overrightarrow{OC}$,求$2x-y$的取值范围.
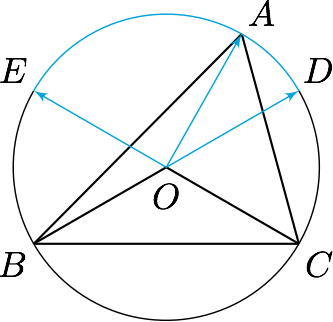
解 设$BD$和$CE$为圆$O$的直径,则点$A$在劣弧$DE$上运动,于是$$\overrightarrow {OA}=(-x)\overrightarrow{OD}+(-y)\overrightarrow{OE},$$且$x,y<0$.
方法一
考虑到问题涉及的代数式为$2x-y$,为了利用向量分解的系数和的几何意义(可以参考每日一题[426] 向量分解的系数和),将条件转化为$$\overrightarrow{OA}=2x\left(-\dfrac 12\overrightarrow{OD}\right)+(-y)\overrightarrow{OE},$$此时可知连接向量$-\dfrac 12\overrightarrow{OD}$的终点$F$与向量$\overrightarrow{OE}$的终点$E$的直线$EF$即等系数和线$$2x-y=1,$$如图.
依次作出其余等系数和线,可得$2x-y$的取值范围是$(-2,1)$.
方法二
根据题意,有$$\overrightarrow {OA}^2=\left[(-x)\overrightarrow{OD}+(-y)\overrightarrow{OE}\right]^2,$$于是$$x^2-xy+y^2=1,$$且$x,y<0$.
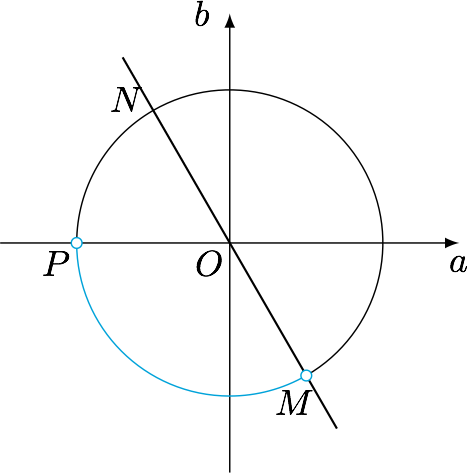
将条件配方,有$$\left(x-\dfrac 12y\right)^2+\left(\dfrac{\sqrt 3}2y\right)^2=1,$$令$$a=x-\dfrac 12y,b=\dfrac{\sqrt 3}2y,$$则所求范围即$2a$的取值范围.根据题意,有$$a+\dfrac{b}{\sqrt 3}<0,b<0,$$规划如图.
不难得到,$a$的取值范围是$\left(-1,\dfrac 12\right)$,因此所求代数式的取值范围是$\left(-2,1\right)$.
方法三
根据外心向量表达(可以参考每日一题[9] “奔驰定理”与五心的向量表达),有$$\sin 2A\overrightarrow{OA}+\sin 2B\overrightarrow{OB}+\sin 2C\overrightarrow{OC}=\overrightarrow 0,$$于是将已知条件整理为$$\dfrac{\sqrt 3}2\overrightarrow{OA}-\dfrac{\sqrt 3}2x\overrightarrow{OB}-\dfrac{\sqrt 3}2y\overrightarrow{OC}=\overrightarrow 0,$$从而可得$$x=-\dfrac{2}{\sqrt 3}\sin 2B,y=-\dfrac{2}{\sqrt 3}\sin 2C.$$
根据题意,有$2C=\dfrac{4\pi}3-2B$.记$2B=\theta$,则$\theta\in\left(\dfrac{\pi}3,\pi\right)$.欲求代数式\[\begin{split} 2x-y&=-\dfrac{4}{\sqrt 3}\sin 2B+\dfrac{2}{\sqrt 3}\sin 2C \\ &=-\dfrac{4}{\sqrt 3}\sin \theta+\dfrac{2}{\sqrt 3}\sin\left(\dfrac{4\pi}3-\theta\right) \\ &=-2\sin \left(\theta+\dfrac{\pi}6\right),\end{split} \]由$\theta$的取值范围不难得到$2x-y$的取值范围是$(-2,1)$.