此题为2016年帷幕第二次群测试题:
设非零向量$\overrightarrow a,\overrightarrow b$满足$\left|\overrightarrow a-\overrightarrow b\right|=2$.设$\overrightarrow a$与$\overrightarrow a -\overrightarrow b$的夹角为$\alpha$,$\overrightarrow b$与$\overrightarrow b- \overrightarrow a$的夹角为$\beta$,有$$4\cos (\alpha+\beta)-\cos(\alpha -\beta )+3=0.$$记$\overrightarrow c= 2\overrightarrow b-\overrightarrow a$,则$\dfrac{\left(\overrightarrow c-\overrightarrow b\right)\cdot \overrightarrow c}{\left|\overrightarrow c\right|}$的最小值为_______.
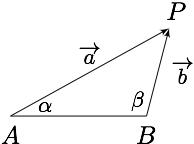
解 如图,三角形$APB$中,$\overrightarrow{AP}=\overrightarrow a$,$\overrightarrow{BP}=\overrightarrow b$,$AB=2$,$\angle BAP=\alpha$,$\angle ABP=\beta$.
由已知条件得$$4\left(2\cos^2\dfrac{\alpha+\beta}2-1\right)-\left(2\cos^2\dfrac{\alpha-\beta}2-1\right)+3=0,$$即$$4\cos^2\dfrac{\alpha+\beta}2=\cos^2\dfrac{\alpha-\beta}2,$$也即$$2\cos\dfrac{\alpha+\beta}2=\cos\dfrac{\alpha-\beta}2,$$两边同乘$2\sin\dfrac{\alpha+\beta}2$,可得$$2\sin(\alpha+\beta)=\sin\alpha+\sin\beta,$$根据正弦定理,有$$PA+PB=2AB=4,$$于是建立下图的直角坐标系后$P$在椭圆$\dfrac{x^2}4+\dfrac{y^2}3=1$上运动(除去长轴端点).
记$\overrightarrow {CP}=\overrightarrow {c}$,则由$\overrightarrow c=2\overrightarrow b-\overrightarrow a$可得$B$为线段$AC$的中点,即$C(3,0)$.所求代数式为$\overrightarrow{CB}$在$\overrightarrow{CP}$上的投影的最小值.由于$BC=2$为定值,于是当$CP$与椭圆相切时,题中代数式取得最小值$2\cos \theta$,其中$\theta=\angle PCB$.
设直线$CP:x-my-3=0$,则由直线与椭圆联立的等效判别式可得$$4+3m^2=9,$$从而$$\tan\angle PCB=\dfrac 1{|m|}=\sqrt{\dfrac 35},$$进而$$2\cos\theta=2\cdot \sqrt{\dfrac 58}=\dfrac{\sqrt {10}}2,$$因此所求最小值为$\dfrac{\sqrt{10}}2$.
注 一般的,对于椭圆的焦点三角形$PF_1F_2$,记$\angle PF_1F_2,\angle PF_2F_1$分别为$\alpha,\beta$,则$$\dfrac{\cos\dfrac{\alpha+\beta}2}{\cos\dfrac{\alpha -\beta}2}=e,$$其中$e$为椭圆的离心率.
对于双曲线的焦点三角形$PF_1F_2$,记$\angle PF_1F_2,\angle PF_2F_1$分别为$\alpha,\beta$,则$$\dfrac{\sin\dfrac{\alpha+\beta}2}{\sin\left|\dfrac{\alpha -\beta}2\right|}=e,$$其中$e$为双曲线的离心率.
这也是题中三角等式的来源.