已知圆$O:x^2+y^2=4$,直线$l:y=kx+5$.
(1)若存在直线$l$上一点$A$以及圆$O$上一点$B$,使得$\angle OAB=\dfrac{\pi}6$,求$k$的取值范围;
(2)若对直线$l$上任意一点$A$,均存在圆$O$上一点$B$,使得$\angle OBA=\dfrac{\pi}6$,求$k$的取值范围.
分析 先不考虑点$A$在直线$l$上这一条件,将注意力都放在当$A$点的位置确定时,随着点$B$的运动,$\angle OAB$或$\angle OBA$的变化范围.
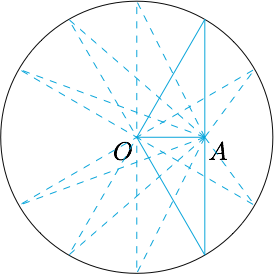
解 (1)当点$A$位于圆$O$内(包含边界)时,显然存在$\angle OAB=\dfrac{\pi}6$.当点$A$位于圆$O$外部时,$\angle OAB$的取值范围是$\left[0,\arcsin\dfrac{2}{OA}\right]$,如图.
因此当$OA\leqslant 4$时,$\angle OAB$可以取得$\dfrac{\pi}6$.回到原问题,即圆心$O$到直线$l$的距离不大于$4$,也即$$\dfrac{5}{\sqrt{1+k^2}}\leqslant 4,$$解得$k$的取值范围是$\left(-\infty,-\dfrac 34\right]\cup\left[\dfrac 34,+\infty\right)$.
(2)当点$A$位于圆$O$外(包含边界)时,显然存在$\angle OBA=\dfrac{\pi}6$.当点$A$位于圆$O$内部时,$\angle OBA$的取值范围是$\left[0,\arcsin\dfrac{OA}{2}\right]$,如图.
因此当$OA\geqslant 1$时,$\angle OBA$可以取得$\dfrac{\pi}6$.回到原问题,即圆心$O$到直线$l$的距离不小于$1$,也即$$\dfrac{5}{\sqrt{1+k^2}}\geqslant 1,$$解得$k$的取值范围是$[-2\sqrt 6,2\sqrt 6]$.