求函数\[f(x)=\cos x+\sqrt{\cos^2x-4\sqrt{2}\cos x+4\sin x+9}\]的最大值与最小值．
首先对函数\(f(x)\)进行代数变形，以期挖掘几何意义：\[f(x)=\cos x+\sqrt{\left(\sqrt 2\cos x-2\right)^2+\left(\sin x+2\right)^2}.\]
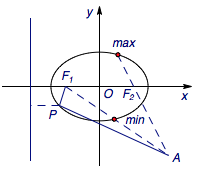
根号下的部分的几何意义比较明显，即椭圆\(\dfrac{m^2}2+n^2=1\)上的点\(P\left(\sqrt 2\cos x,\sin x\right)\)到点\(A\left(2,-2\right)\)的距离，那么剩下的\(\cos x\)的几何意义是什么呢？
注意到椭圆的左准线为\(x=-2\)和\(x=2\)，离心率\(e=\dfrac{\sqrt 2}2\)，于是\(P\)到左焦点的距离为\[PF_1=\dfrac{\sqrt 2}2\left(\sqrt 2\cos x+2\right)=\cos x+\sqrt 2.\]
因此我们有\[\begin{split}f(x)&=PF_1+PA-\sqrt 2\\&\geqslant F_1A-\sqrt 2=\sqrt{13}-\sqrt 2.\end{split}\]
另一方面，由椭圆的定义，有\[\begin{split}f(x)&=\left(2\sqrt 2-PF_2\right)+PA-\sqrt 2\\&=PA-PF_2+\sqrt 2\\&\leqslant AF_2+\sqrt 2=\sqrt 5+\sqrt 2.\end{split}\]
于是函数\[f(x)=\cos x+\sqrt{\cos^2x-4\sqrt{2}\cos x+4\sin x+9}\]的最大值与最小值分别为\(\sqrt 5+\sqrt 2\)和\(\sqrt{13}-\sqrt 2\)．
最后，我们用一道高考题作为练习题．
求函数\(f(x)=\dfrac{\left|\sin x-1\right|}{\sqrt{3-2\sin x-2\cos x}}\)的值域．
参考答案 \(\left[0,1\right]\)．
提示 \(f(x)=\dfrac{1}{\sqrt{1+\left(\dfrac{1-\cos x}{1-\sin x}\right)^2}}\)．
妙啊