这是我在QQ群中国数学解题研究会中看到的问题:
已知平面向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$满足$\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}$($x,y\in\mathcal R$),且$\overrightarrow{a}\cdot\overrightarrow{c}>0$,$\overrightarrow {b}\cdot\overrightarrow{c}>0$.
A.若$\overrightarrow{a}\cdot\overrightarrow{b}<0$,则$x>0$,$y>0$
B.若$\overrightarrow{a}\cdot\overrightarrow{b}<0$,则$x<0$,$y<0$
C.若$\overrightarrow{a}\cdot\overrightarrow{b}>0$,则$x>0$,$y>0$
D.若$\overrightarrow{a}\cdot\overrightarrow{b}>0$,则$x<0$,$y<0$
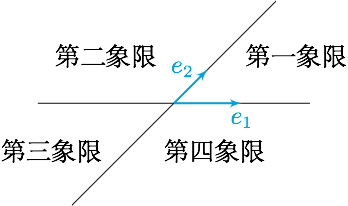
分析 我们知道,对于给定的一组基底,可以类比于平面直角坐标系定义对应的四个“象限”,如图.
其中$\overrightarrow{c}$的终点位于“第一象限”中时满足$x>0$且$y>0$,位于“第二象限”中时满足$x<0$且$y>0$,依次类推.
解 题意即若$\overrightarrow{c}$与$\overrightarrow{a}$和$\overrightarrow{b}$的夹角均为锐角或零角.
于是若$\overrightarrow{a}\cdot\overrightarrow{b}\leqslant 0$,那么$\overrightarrow{c}$的终点必然在“第一象限”;
若$\overrightarrow{a}\cdot\overrightarrow{b}>0$,那么$\overrightarrow{c}$可能在“第一、二、四象限”.
因此正确的答案是 A.
注 讨论过程中所有向量均默认以原点为起点.