这是我在QQ群中国数学解题研究会中看到的题目:
对于函数$f(x)$,若存在$x_0\in\mathcal Z$,满足$\left|f(x_0)\right|\leqslant \dfrac 14$,则称$x_0$为函数$f(x)$的一个“近零点”.已知函数$f(x)=ax^2+bx+c$($a>0$)有四个不同的“近零点”,则$a$的最大值为_______.
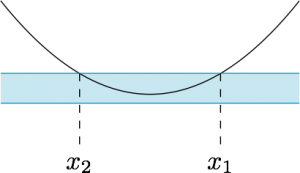
分析 题意即抛物线$y=f(x)$在平行线$y=\dfrac 14$和$y=-\dfrac 14$之间的部分(含边界),在$x$轴上的投影覆盖$4$个整点.因此应该从分析方程$f(x)=\dfrac 14$和方程$f(x)=-\dfrac 14$的解入手.
解 方程$f(x)=\dfrac 14$必然有两个不同实根,设为$x_1,x_2$,且$x_1>x_2$.
第一种情况,方程$f(x)=-\dfrac 14$没有根或有两个重根.
此时$b^2-4ac-a\leqslant 0$.抛物线在两条平行线间的部分在$x$轴上的投影为$[x_2,x_1]$,因此$$x_1-x_2=\dfrac{\sqrt{b^2-4ac+a}}a\geqslant 3,$$又$$\dfrac{\sqrt{b^2-4ac+a}}a\leqslant \dfrac{\sqrt {2a}}{a},$$于是可得$$\dfrac{\sqrt {2a}}{a}\geqslant 3,$$从而$a\leqslant \dfrac 29$.
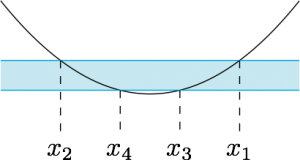
第二种情况,方程$f(x)=-\dfrac 14$有两个不同实根.
不妨设两根分别为$x_3,x_4$,且$x_3>x_4$,此时$b^2-4ac-a>0$,且抛物线在两条平行线间的部分在$x$轴上的投影为$[x_2,x_4]\cup[x_3,x_1]$,因此有$$\begin{cases} (x_1-x_2)-(x_3-x_4)\geqslant 2,\\ x_1-x_2\geqslant 3,\end{cases} $$即$$\begin{cases} \sqrt{b^2-4ac+a}+\sqrt{b^2-4ac-a}\leqslant 1,\\ b^2-4ac\geqslant 9a^2-a,\end{cases} $$进而可得$$3a+\sqrt{9a^2-2a}\leqslant 1,$$解得$$\dfrac 29\leqslant a \leqslant \dfrac 14.$$
综上所述,有$a\leqslant \dfrac 14$.接下来证明$a$可以取得$\dfrac 14$.
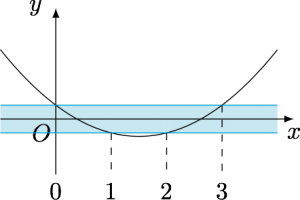
我们可以尝试四个“近零点”分别为$0,1,2,3$,这样可以设$$f(x)=a\left(x-\dfrac 32\right)^2+h,$$则$$\begin{cases} f(0)=\dfrac 94a+h=\dfrac 14,\\ f(1)=\dfrac 14a+h=-\dfrac 14,\end{cases} $$解得$a=\dfrac 14$,$h=-\dfrac {5}{16}$,如图.
这样,我们就得到$a$的最大值为$\dfrac 14$.