每日一题[366]数形结合

已知函数$f(x)=\begin{cases} -x^2+ax,x\leqslant 1,\\ax-1,x>1,\end{cases}$，若$\exists x_1,x_2\in\mathcal{R},x_1\ne x_2$，使$f(x_1)=f(x_2)$成立，则实数$a$的取值范围是_____．

正确答案是$a<2$．

解　$f(x)$是分段函数，题中条件“$\exists x_1,x_2\in\mathcal{R},x_1\ne x_2,$，使$f(x_1)=f(x_2)$成立”，即“函数$f(x)$不是单调函数”．考虑到右半段的单调性，找到讨论分界点$0$：

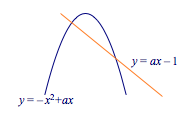
当$a<0$时，函数左半段（$x\leqslant 1$时）为开口向下的抛物线，右半段是斜率为负的直线，函数一定不单调，如图，始终满足题意；

当$a=0$时，显然满足题意；

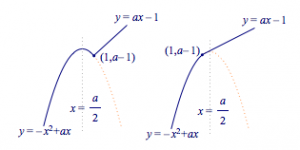
当$a>0$时，左半段是开口向下的抛物线，且对称轴为$x=\dfrac a2$，取抛物线上$x\leqslant 1$的一段，再从点$(1,a-1)$上作斜率为$a>0$的直线，如下图：

由图象知，当$\dfrac a2<1$时，满足条件，故$0<a<2$；

综上知，$a$的取值范围为$a<2$．