若实数$x,y$满足$x\geqslant -1,y\geqslant -1$,且$2^x+2^y=4^x+4^y$,求$2^{2x-y}+2^{2y-x}$的取值范围.
正确答案是$\left[2,1+\dfrac {3\sqrt 2}{2}\right ]$.
解 设$2^x=a,2^y=b$,则$a,b\geqslant \dfrac 12$,且$$\begin{eqnarray} a^2+b^2=a+b\end{eqnarray} $$记所求代数式为$M$,则\[M=\dfrac {b^2}{a}+\dfrac {a^2}{b}.\]
方法一 (由意琦行提供)
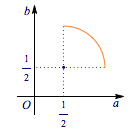
考虑对$M$进行代数变形,将$M$化成齐次式有\[M=\dfrac{a^3+b^3}{ab}\cdot\dfrac{a+b}{a^2+b^2}.\]令$t=\dfrac ab$,有\[\begin{split} M&=\dfrac {(t^3+1)(t+1)}{t(t^2+1)}\\&=\dfrac {(t+1)^2}{t}\cdot\dfrac {t^2-t+1}{t^2+1}\\&=\left(t+\dfrac 1t+2\right )\cdot\left(1-\dfrac {1}{t+\frac 1t}\right ).\end{split} \]令$s=t+\dfrac 1t$,于是得$$\begin{eqnarray} M=(s+2)\left(1-\dfrac 1s\right)=1+s-\dfrac 2s.\end{eqnarray} $$(1)的限制条件为$$\left(a-\dfrac 12\right )^2+\left(b-\dfrac 12\right )^2=\dfrac 12,$$于是$(a,b)$在一个$\dfrac 14$圆弧上(包括端点),如图:
从而有$\dfrac ab\in\left[\sqrt 2-1,\sqrt 2+1\right ]$,$s\in \left[2,2\sqrt 2\right]$.
代入(2)式得$M$的范围是$$\left[2,1+\dfrac {3\sqrt 2}{2}\right ].$$
方法二 由(1)知可以令\[\begin{cases} a=\dfrac 12+\dfrac {\sqrt 2}{2}\cos\theta,\\b=\dfrac 12+\dfrac {\sqrt 2}{2}\sin\theta,\end{cases} \theta\in\left[0,\dfrac {\pi}{2}\right ].\]代入$M$中化简得\[M=\dfrac{\left[2+\sqrt 2(\sin\theta+\cos\theta)\right]\cdot\left[3+\sqrt 2(\sin\theta+\cos\theta)-2\sin\theta\cos\theta\right]}{2\left[1+\sqrt 2(\sin\theta+\cos\theta)+2\sin\theta\cos\theta\right]}.\]令$t=\sin\theta+\cos\theta$,则$t=\sqrt 2\sin\left(\theta+\dfrac{\pi}{4}\right )\in [1,\sqrt 2]$,且$2\sin\theta\cos\theta=t^2-1$.
代入前面式子得$$M=\dfrac {\sqrt 2}{2}\left(\dfrac 4t-t\right )+1\in\left[2,1+\dfrac 32\sqrt 2\right ].$$
注 方法一从所求代数式入手,尝试齐次化后用均值不等式或者转化成函数的值域去求解,这也是常用的思考方向;方法二从题目的条件入手,根据条件的意义考虑通过换元将两个变量的问题转化成单变量的问题.
在本题中,因为条件比较特殊,也可以考虑对称性直接通过边界与对称点得到所求代数式的范围,将$M$进行变形\[\begin{split} M&=\dfrac {a+b-b^2}{b}+\dfrac {a+b-a^2}{a}\\&=\dfrac ab+\dfrac ba-(a+b)+2.\end{split} \]结合$(a,b)$在圆弧上容易得到$$\dfrac ab+\dfrac ba\in[2,2\sqrt 2],a+b\in \left[1+\dfrac {\sqrt 2}{2},2\right ],$$从而$$M\in\left[2,1+\dfrac 32\sqrt 2\right ],$$且边界恰好可以取到,于是得到$M$的取值范围.但这种方法没有一般性,条件稍作改变就无法奏效.