2015高考数学湖北文科第10题(选择压轴题):
已知集合$A=\left\{\left(x,y\right) \left|\right. x^2+y^2\leqslant 1,x,y\in{\mathcal{Z}}\right\}$,$B=\left\{(x,y) \big||x|\leqslant 2,|y|\leqslant 2,x,y\in{\mathcal{Z}}\right\}$,定义集合$A\oplus B=\left\{\left(x_1+x_2,y_1+y_2\right) \left|\right. \left(x_1,y_1\right)\in A,\left(x_2,y_2\right)\in B\right\}$,则$A\oplus B$中元素的个数为____.
正确答案是$45$.
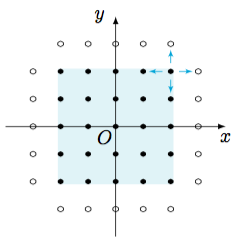
解 集合$A$包含$5$个元素$$\{(0,1),(0,-1),(-1,0),(1,0),(0,0)\},$$而集合$B$表示一个$5\times 5$的点阵.根据$A\oplus B$的定义可知,如果将$A\ \oplus$理解为某个操作,那么这个操作作用于单个点时,就是将这个点向上、向下、向左、向右平移一个单位以及维持不动后得到$5$个点.于是当$A\oplus$作用于一个点集时,就是将这个点集向上、向下、向左、向右平移一个单位以及维持不动后得到新的点集,如图.
不难得到,新的点集比原来多出$20$个点,因此共有$45$个元素.
下面我们给出一道练习:
集合$A$及两个集合的$\oplus$定义同上,如果集合$C=\left\{(x,y) \big||x|+|y|\leqslant 2,x,y\in{\mathcal{Z}}\right\}$,则$A\oplus C$中元素的个数为____.
答案 $25$.
更进一步,可以思考,如果集合$C_n=\left\{(x,y) \big||x|+|y|\leqslant n,x,y\in{\mathcal{Z}}\right\}$,其中$n\in\mathcal{N}^*$,则$A\oplus C_n$中的元素个数为多少?
答案是$2n^2+6n+5$.
相关问题见每日一题[325]平面区域,在那个问题里集合$A,B$是平面区域,不是离散的点集.