每日一题[325]平面区域

在平面直角坐标系中，点集$A=\{(x,y)|x^2+y^2\leqslant 1\}$，$B=\{(x,y)|x\leqslant 4,y\geqslant 0,3x-4y\geqslant 0\}$，则

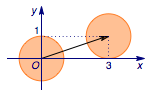
（1）点集$P=\{(x,y)|x=x_1+3,y=y_1+1,(x_1,y_1)\in A\}$所表示的平面区域的面积为____；

（2）点集$Q=\{(x,y)|x=x_1+x_2,y=y_1+y_2,(x_1,y_1)\in A,(x_2,y_2)\in B\}$所表示的平面区域的面积为____．

正确答案是（1）$\pi$；（2）$18+\pi$．

解　（1）从点$M(x,y)$得到点 $M'(x+3,y+1)$相当于将点$M$向右平移$3$个单位，再向上平移$1$个单位．

根据点集$P$的定义知，点集$P$就是将点集$A$中的任意一个点向右平移$3$个单位，再向上平移$1$个单位得到的，所以直接将点集$A$表示的平面区域作这样的平移就能得到点集$P$．

点集$A$是以原点为圆心的单位圆，所以点集$P$就是以$(3,1)$为圆心，半径为$1$的圆，面积为$\pi$，如图：

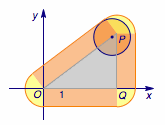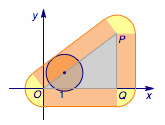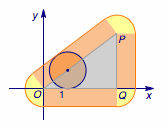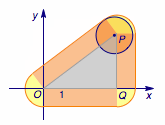
（2）在点集$Q$中，横坐标是由两个变化的数共同决定的，纵坐标也是由两个变化的数共同决定的，受（1）的启发，可以先取定一点$M(x_2,y_2)\in B$，让$(x_1,y_1)\in A$变化，由此得到的平面区域是点集$Q$的一部分，再让$M(x_2,y_2)$在区域$B$中运动起来，就可以得到整个点集$Q$表示的区域．

由（1）知，取定$M(x_2,y_2)\in B$时，得到的点集是以$M$为圆心，以$1$为半径的圆．当$M$在区域$B$中运动起来，这些单位圆（及其内部）运动扫过的区域就是所求的平面区域．$B$是如下的三角形$OPQ$及其内部构成的区域，其中$P(4,3),Q(4,0)$，只需考虑$M$在边界三角形$OPQ$上的运动即可，得到的边界及其内部就是$Q$表示的平面区域，如图：

容易计算所求面积为$18+\pi$．

在动态问题中，先固定一个变元，让另一个变元动起来，得到一个中间状态，再让固定的变元动起来，是常见的处理思路．