每日一题[322]三点共线

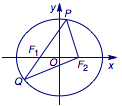
已知$F_1,F_2$是椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$的焦点，直线$PQ$过$F_1$且交椭圆于$P$、$Q$两点．若$PF_1=F_1F_2$，且$2PF_1=3QF_1$，求椭圆的离心率．

---

正确答案是$\dfrac {\sqrt{41}-4}{5}$．

解　不妨设$F_1F_2=2c=6$，则$PF_1=F_1F_2=6$，$PF_2=2a-PF_1=2a-6$,$QF_1=\dfrac 23 PF_1=4$，$QF_2=2a-QF_1=2a-4$．

由于$\angle PF_1F_2$与$\angle QF_1F_2$互补，所以

$$\cos \angle PF_1F_2+\cos \angle QF_1F_2=0,$$ 即 $$\dfrac{36+36-(2a-6)^2}{2\times 6\times 6}+\dfrac{16+36-(2a-4)^2}{2\times 4\times 6}=0.$$ 化简得 $$5a^2-24a-45=0,$$ 解得 $$a=\dfrac{12+3\sqrt{41}}5.$$ 所以 $$e=\dfrac ca=\dfrac{15}{12+3\sqrt{41}}=\dfrac{\sqrt{41}-4}{5}.$$

本题解题的关键是如何处理条件直线$PQ$过点$F_1$，即$P,F_1,Q$三点共线．因为本题已经用一个未知数表示出两个三角形的各条边的长度，所以表达三点共线转化成两个三角形中有一个内角互补，从而利用余弦定理得到了等式．

注　本题中因为$a,b,c$成比例放大或缩小不影响题中的线段长度的比例关系，也不影响离心率，所以可以取$c=3$，简化运算．