每日一题[51] 划清界限得范围

今天的题目是2015年北京市东城区高三期末理科数学选择题的最后一题．

已知圆\(C:x^2+y^2=2\)，直线\(l:x+2y-4=0\)，点\(P\left(x_0,y_0\right)\)在直线\(l\)上．若存在圆\(C\)上的点\(Q\)，使得\(\angle OPQ=45^\circ\)（\(O\)为坐标原点），则\(x_0\)的取值范围是（        ）

A．\([0,1]\)

B．\(\left[0,\dfrac 85\right]\)

C．\(\left[-\dfrac 12,1\right]\)

D．\(\left[-\dfrac 12,\dfrac 85\right]\)

 正确答案是B．

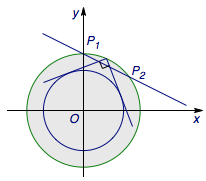
首先寻找对圆的视角等于\(90^\circ\)的点的轨迹，显然这是一个封闭曲线（事实上这个封闭曲线是圆，半径为\(2\)，想一想为什么？）．那么在圆内部的点对圆的视角均大于\(90^\circ\)，也即使得\(\angle OPQ=45^\circ\)的点；同时在圆外部的点对圆的视角均小于\(90^\circ\)，一定不可能使得\(\angle OPQ=45^\circ\)．

由此分析不难得出，所求点\(P\)的取值集合为直线\(l:x+2y-4=0\)被圆\(x^2+y^2=4\)所截得的线段\(P_1P_2\)．

设\(P\left(x_0,\dfrac 12\left(4-x_0\right)\right)\)，则\[x_0^2+\frac 14\left(4-x_0\right)^2=4,\]解得\[x_0=0\lor x_0=\frac 85.\]