每日一题[307] 清君侧，靖国难

这是我的好朋友凌落蓝提供的一道试题：

已知$f(x)=\dfrac{1+\ln x}{x-1}$，$g(x)=\dfrac kx$（$k\in\mathcal N^*$）．若对任意$c>1$，均存在$a,b$满足$0<a<b<c$，使得$f(c)=f(a)=g(b)$，则$k$的最大值为_______．

正确的答案是$3$．

解    先研究函数$f(x)$，其导函数$$f'(x)=-\dfrac{1+x\ln x}{x(x-1)^2},$$又$$\left(1+x\ln x\right)'=1+\ln x,$$于是$1+x\ln x$的最小值为$$1+\dfrac{1}{\rm e} \cdot\ln \dfrac 1{\rm e} >0,$$因此$f(x)$在$(0,1)$和$(1,+\infty)$上分别单调递减．

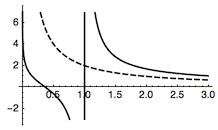
根据题意，函数$g(x)=\dfrac kx$的图象夹在$f(x)$图象在$x<1$和$x>1$的两个部分之间，也即$$\begin{cases} \forall x\in (0,1),\dfrac kx>\dfrac{1+\ln x}{x-1},\\\forall x\in (1,+\infty ),\dfrac kx<\dfrac{1+\ln x}{x-1}, \end{cases} $$即$$\forall x>0\land x\ne 1,1+\ln x>\dfrac{k(x-1)}{x},$$也即$$\forall x>0\land x\ne 1,1+\ln x+\dfrac kx-k>0,$$设不等式左边函数为$h(x)$，则$h(x)$的导函数$$h'(x)=\dfrac{x-k}{x^2},$$于是当$x=k$时，$h(x)$有最小值$$h(k)=\ln k-k+2\geqslant 0,$$由$$\left(\ln k-k+2\right)'_k=\dfrac 1k-1\leqslant 0,$$于是$h(k)$随着正整数$k$的增大而减小，不难验证得知$k$的最大值为$3$．

从此题中可以看到，处理包含对数函数$\ln x$的问题时，可以考虑先将与$\ln x$相乘的因式消灭（即“清君侧”），从而避免求导后仍然包含对数符号而需要再次求导的问题（即“靖国难”）．

注    更多的例题可以参考《每日一题[49] 分离对数函数》．