每日一题[299] 分段与分离相遇

2015年北京市海淀区高三期中理科数学第8题（选择压轴题）：

已知函数$f(x)=\begin{cases} -1,x\leqslant -1,\\x,-1<x<1,\\1,x \geqslant 1,\end{cases}$函数$g(x)=ax^2-x+1$．若函数$y=f(x)-g(x)$恰好有$2$个不同零点，则实数$a$的取值范围是（        ）

A．$(0,+\infty )$

B．$(-\infty ,0)\cup (2,+\infty )$

C．$\left( -\infty ,-\dfrac 12\right) \cup (1,+\infty )$

D．$(-\infty ,0)\cup (0,1)$

---

正确答案是 D．

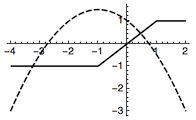
解    如果直接考虑函数$f(x)$与函数$g(x)$的图象的交点个数会比较麻烦，如图1．

实际上，对于分段函数，我们仍然可以考虑分离变量，根据题意，方程

$$f(x)=ax^2-x+1$$ 有两根，即 $$ax^2-x+1=\begin{cases} -1,x\leqslant -1,\\x,-1<x<1,\\1,x \geqslant 1,\end{cases}$$ 有两根，注意到$x=0$不是方程的根，于是问题即方程 $$a=\begin{cases} \dfrac 1x-\dfrac 2{x^2},x\leqslant -1,\\\dfrac 2x-\dfrac 1{x^2},-1<x<0\lor 0<x<1,\\\dfrac 1x,x\geqslant 1\end{cases}$$ 有两根．

作换元$t=\dfrac 1x$，则上述方程右边

$$g(t)=\begin{cases} t-2t^2,-1\leqslant t<0,\\2t-t^2,t<-1\lor t>1,\\t,0<t\leqslant 1,\end{cases}$$ 而换元后的方程的根的个数与换元前的方程的根的个数是一致的．

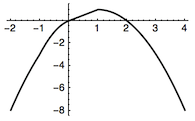
考虑函数$y=g(t)$与直线$y=a$的交点个数，如图2：

于是$a$的取值范围是$a<1\land a\neq 0$，也即$(-\infty ,0)\cup (0,1)$．

从本题可以看出，分离参数处理函数的零点问题的手段不会因为函数是分段函数的形式而失效．

注    也可以半分离参数为

$$ax=\begin{cases} \dfrac{x-2}x,x\leqslant -1,\\\dfrac {2x-1}x,-1<x<0\lor 0<x<1,\\1,x\geqslant 1.\end{cases}$$